
题目列表(包括答案和解析)
已知函数 ,
, .
.
(Ⅰ)若函数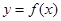 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
【解析】第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式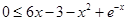 在
在 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为 ,有
,有 .
.
故 在区间
在区间 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又 [来源:]
[来源:]

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
已知函数 .(
.( )
)
(1)若 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
【解析】第一问中,首先利用 在区间
在区间 上单调递增,则
上单调递增,则 在区间
在区间 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间 上单调递增,
上单调递增,
则 在区间
在区间 上恒成立. …………3分
上恒成立. …………3分
即 ,而当
,而当 时,
时, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令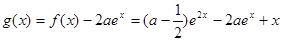 ,定义域为
,定义域为 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,
,
当 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有 ,不合题意;
,不合题意;
当 ,即
,即 时,同理可知,
时,同理可知, 在区间
在区间 上递增,
上递增,
有 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若 ,则有
,则有 ,此时在区间
,此时在区间 上恒有
上恒有 ,从而
,从而 在区间
在区间 上是减函数;
上是减函数;
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是
的范围是 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
如图, 是△
是△ 的重心,
的重心, 、
、 分别是边
分别是边 、
、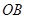 上的动点,且
上的动点,且 、
、 、
、 三点共线.
三点共线.
(1)设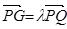 ,将
,将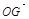 用
用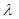 、
、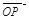 、
、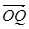 表示;
表示;
(2)设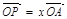 ,
,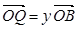 ,证明:
,证明: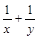 是定值;
是定值;
(3)记△ 与△
与△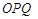 的面积分别为
的面积分别为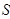 、
、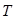 .求
.求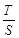 的取值范围.
的取值范围.
(提示: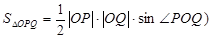
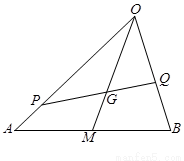
【解析】第一问中利用(1)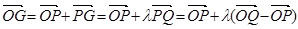
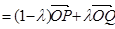
第二问中,由(1),得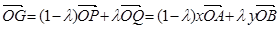 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴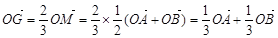
而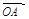 、
、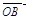 不共线,∴由①、②,得
不共线,∴由①、②,得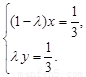
第三问中,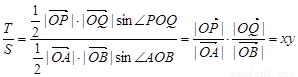
由点 、
、 的定义知
的定义知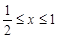 ,
,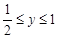 ,
,
且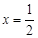 时,
时,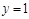 ;
;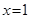 时,
时,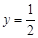 .此时,均有
.此时,均有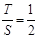 .
.
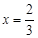 时,
时,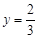 .此时,均有
.此时,均有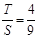 .
.
以下证明: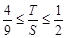 ,结合作差法得到。
,结合作差法得到。
解:(1)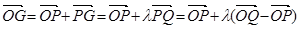
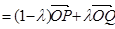 .
.
(2)一方面,由(1),得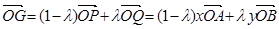 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴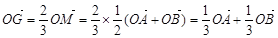 . ②
. ②
而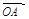 、
、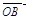 不共线,∴由①、②,得
不共线,∴由①、②,得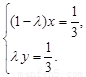
解之,得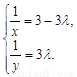 ,∴
,∴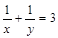 (定值).
(定值).
(3)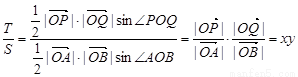 .
.
由点 、
、 的定义知
的定义知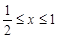 ,
,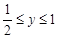 ,
,
且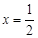 时,
时,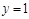 ;
;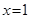 时,
时,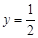 .此时,均有
.此时,均有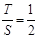 .
.
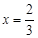 时,
时,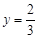 .此时,均有
.此时,均有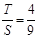 .
.
以下证明: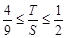 .(法一)由(2)知
.(法一)由(2)知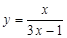 ,
,
∵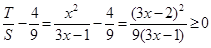 ,∴
,∴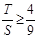 .
.
∵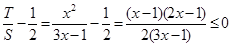 ,∴
,∴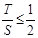 .
.
∴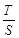 的取值范围
的取值范围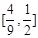
(09年东城区二模理)(14分)
已知函数![]() =
=![]() (其中
(其中![]() 为常数,
为常数,![]() ).利用函数
).利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:
,方法如下:
对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述构造过程中,如果![]() (
(![]() =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果![]() 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(Ⅰ)当![]() 且
且![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)如果可以用上述方法构造出一个常数列,求![]() 的取值范围;
的取值范围;
| 消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900) | … |
| 第二次优惠金额(元) | 30 | 60 | 100 | 150 | … |
| 购买商品获得的优惠总额 |
| 商品的标价 |
| 1 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com