
题目列表(包括答案和解析)
三、解答题. (本大题共6题,第17-21题每题12分,第22题14分)
17、(本小题满分12分)
某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
(2012年高考辽宁卷理科20) (本小题满分12分)
如图,椭圆![]() ,动圆
,动圆![]() .点
.点![]() 分
分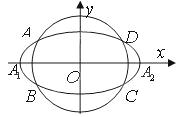 别为
别为![]() 的左、右顶点,
的左、右顶点,![]() 与
与![]() 相交于
相交于![]() 四点
四点
(1)求直线![]() 与直线
与直线![]() 交点
交点![]() 的轨迹方程;
的轨迹方程;
(2)设动圆![]() 与
与![]() 相交于
相交于![]() 四点,其中
四点,其中![]() ,
,![]() .若矩形
.若矩形![]() 与矩形
与矩形![]() 的面积相等,证明:
的面积相等,证明:![]() 为定值
为定值
三、解答题. (本大题共6题,第17-21题每题12分,第22题14分)
17、(本小题满分12分)
某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当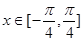 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(本小题满分12分)
某班全部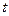 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。
| 分 组 | 频数 | 频率 |
| [13,14) |  | 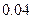 |
| [14,15) | 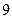 | 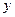 |
| [15,16) | 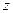 |  |
| [16,17) | 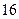 | 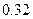 |
| [17,18] | 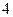 | 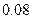 |
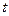 及上表中的
及上表中的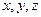 的值;
的值; 百米测试成绩,求事件“
百米测试成绩,求事件“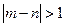 ”的
”的 概率.
概率.
一、1―5 DDDBB 6―10 CABCA 11―12 CD
二、13.试题(全国).files/image121.gif)
14.甲 15.12,3 16.试题(全国).files/image123.gif)
三、17.解:
(1)∵试题(全国).files/image125.gif)
=试题(全国).files/image127.gif)
=试题(全国).files/image129.gif)
=试题(全国).files/image131.gif)
=试题(全国).files/image133.gif)
∴周期试题(全国).files/image135.gif)
(2)∵试题(全国).files/image137.gif)
因为试题(全国).files/image139.gif) 在区间
在区间试题(全国).files/image141.gif) 上单调递增,
上单调递增,
在区间试题(全国).files/image143.gif) 上单调递减,
上单调递减,
所以,当试题(全国).files/image145.gif) 时,
时,试题(全国).files/image094.gif) 取最大值1
取最大值1
又试题(全国).files/image148.gif)
∴当试题(全国).files/image150.gif) 时,
时,试题(全国).files/image094.gif) 取最小值
取最小值试题(全国).files/image152.gif)
所以函数试题(全国).files/image094.gif) 在区间
在区间试题(全国).files/image154.gif) 上的值域为
上的值域为试题(全国).files/image156.gif)
18.证明:
(Ⅰ)连接AC,则F是AC的中点,在△CPA中,EF∥PA…………………………3分
且PC试题(全国).files/image158.gif) 平面PAD,EF
平面PAD,EF试题(全国).files/image160.gif) PAD,
PAD,
∴EF∥平面PAD…………………………………………………………………………6分
(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,
∴CD⊥平面PAD,∴CD⊥PA…………………………………………………………8分
又PA=PD=试题(全国).files/image162.gif) AD,∴△PAD是等腰直角三角形,且∠APD=
AD,∴△PAD是等腰直角三角形,且∠APD=试题(全国).files/image164.gif)
即PA⊥PD………………………………………………………………………………10分
而CD∩PD=D,∴PA⊥平面PDC,又EF∥PA,∴EF⊥平面PDC………………12分
19.(I)由试题(全国).files/image166.gif) ①
①
试题(全国).files/image168.gif) ②
②
①-②得:试题(全国).files/image170.gif)
即试题(全国).files/image172.gif)
试题(全国).files/image174.gif)
试题(全国).files/image176.gif)
试题(全国).files/image178.gif)
(II)试题(全国).files/image180.gif)
试题(全国).files/image182.gif)
试题(全国).files/image184.gif)
试题(全国).files/image186.gif)
试题(全国).files/image188.gif)
故试题(全国).files/image109.gif)
20.解:(1)试题(全国).files/image191.gif)
(2)试题(全国).files/image193.gif)
试题(全国).files/image195.gif)
由试题(全国).files/image197.gif) 及bc=20与a=3
及bc=20与a=3
解得b=4,c=5或b=5,c=4
(3)设D到三边的距离分别为x、y、z
则试题(全国).files/image199.gif)
试题(全国).files/image201.gif)
又x、y满足试题(全国).files/image203.gif)
画出不等式表示的平面区域得:试题(全国).files/image205.gif)
21.解:(1)试题(全国).files/image207.gif)
由于函数试题(全国).files/image115.gif) 时取得极值,
时取得极值,
所以试题(全国).files/image210.gif)
即试题(全国).files/image212.gif)
(2)方法一
由 题设知:试题(全国).files/image214.gif)
对任意试题(全国).files/image216.gif) 都成立
都成立
即试题(全国).files/image218.gif) 对任意
对任意试题(全国).files/image216.gif) 都成立
都成立
设试题(全国).files/image220.gif) ,
,
则对任意试题(全国).files/image222.gif) 为单调递增函数
为单调递增函数试题(全国).files/image224.gif)
所以对任意试题(全国).files/image226.gif) 恒成立的充分必要条件是
恒成立的充分必要条件是试题(全国).files/image228.gif)
即试题(全国).files/image230.gif)
于是x的取值范围是试题(全国).files/image232.gif)
方法二
由题设知:试题(全国).files/image214.gif)
对任意试题(全国).files/image216.gif) 都成立
都成立
即试题(全国).files/image218.gif)
对任意试题(全国).files/image216.gif) 都成立
都成立
于是试题(全国).files/image236.gif) 对任意
对任意试题(全国).files/image216.gif) 都成立,
都成立,
即试题(全国).files/image238.gif)
试题(全国).files/image240.gif)
于是x的取值范围是试题(全国).files/image232.gif)
22.解:(I)由题意设椭圆的标准方程为试题(全国).files/image242.gif)
由已知得:试题(全国).files/image244.gif)
试题(全国).files/image246.gif)
试题(全国).files/image248.gif) 椭圆的标准方程为
椭圆的标准方程为试题(全国).files/image250.gif)
(II)设试题(全国).files/image252.gif)
联立试题(全国).files/image254.gif)
得试题(全国).files/image256.gif)
试题(全国).files/image258.gif)
又试题(全国).files/image260.gif)
因为以AB为直径的圆过椭圆的右焦点D(2,0)
∴试题(全国).files/image262.gif)
∴试题(全国).files/image264.gif) +
+ 试题(全国).files/image266.gif) -2
-2试题(全国).files/image268.gif)
∴试题(全国).files/image270.gif)
∴试题(全国).files/image272.gif)
解得:
试题(全国).files/image274.gif) 且均满足
且均满足试题(全国).files/image276.gif)
当试题(全国).files/image278.gif) ,直线过定点(2,0)与已知矛盾;
,直线过定点(2,0)与已知矛盾;
当试题(全国).files/image280.gif) 时,l的方程为
时,l的方程为试题(全国).files/image282.gif) ,直线过定点(
,直线过定点(试题(全国).files/image284.gif) ,0)
,0)
所以,直线l过定点,定点坐标为(试题(全国).files/image284.gif) ,0)
,0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com