
题目列表(包括答案和解析)
某港口的水深![]() (米)是时间
(米)是时间![]() (0≤
(0≤![]() ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:

根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数![]() 的图像.
的图像.

(1)试根据以上数据,求出![]() 的表达式;
的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间?(忽略进出港所用的时间)?
 (米)是时间
(米)是时间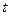 (0≤
(0≤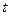 ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:
 的图像.
的图像.
 的表达式;
的表达式;t(小时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
经长期观察,y=f(t)的曲线可以近似地看成函数y=Asinωx+b的图象.
(1)试根据以上数据,求出函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水深度(船底离水面的距离)为6.5米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港时间)?
受日月引力的作用,海水会发生涨落,这种现象叫潮汐. 在通常情况下,船在海水涨潮时驶进航道,靠近码头,卸货后返回海洋.某港口水的深度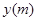 是时间
是时间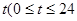 ,单位:
,单位: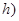 的函数,记作:
的函数,记作: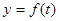 ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:

经过长期观察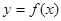 的曲线可以近似地看做函数
的曲线可以近似地看做函数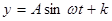 的图象.
的图象.
(Ⅰ)根据以上数据,求出函数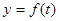 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时船底离海底的距离为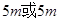 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为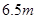 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
受日月引力的作用,海水会发生涨落,这种现象叫潮汐. 在通常情况下,船在海水涨潮时驶进航道,靠近码头,卸货后返回海洋.某港口水的深度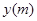 是时间
是时间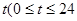 ,单位:
,单位: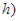 的函数,记作:
的函数,记作: ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
经过长期观察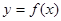 的曲线可以近似地看做函数
的曲线可以近似地看做函数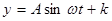 的图象.
的图象.
(Ⅰ)根据以上数据,求出函数 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时船底离海底的距离为 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为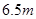 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
一、选择题:DBDBD CABCA AC
二、填空题
13.5
14.2
15.旧人教.files/image178.gif)
16.①②④
17.解:(1)旧人教.files/image180.gif)
旧人教.files/image182.gif)
(2)旧人教.files/image184.gif)
旧人教.files/image186.gif)
旧人教.files/image188.gif)
旧人教.files/image190.gif)
旧人教.files/image192.gif)
18.解:旧人教.files/image194.gif)
旧人教.files/image196.gif)
旧人教.files/image198.gif) 又
又旧人教.files/image200.gif)
旧人教.files/image202.gif)
旧人教.files/image204.gif)
旧人教.files/image206.gif)
19.解:(1)旧人教.files/image208.gif)
当旧人教.files/image210.gif)
即旧人教.files/image212.gif) 时,
时,旧人教.files/image167.gif) 为增函数
为增函数
(2)当旧人教.files/image215.gif) 时,
时,旧人教.files/image217.gif)
旧人教.files/image219.gif) ,
,
旧人教.files/image221.gif)
旧人教.files/image223.gif)
旧人教.files/image225.gif)
当旧人教.files/image227.gif) 时,
时,旧人教.files/image229.gif)
即旧人教.files/image231.gif)
又旧人教.files/image233.gif)
旧人教.files/image235.gif)
20.解(1)已知等差数列旧人教.files/image237.gif)
旧人教.files/image239.gif)
(2)当旧人教.files/image241.gif)
旧人教.files/image243.gif)
(3)由题意,旧人教.files/image245.gif)
旧人教.files/image247.gif)
旧人教.files/image249.gif)
旧人教.files/image251.gif) 是一个单调增数列,要
是一个单调增数列,要旧人教.files/image253.gif) 恒成立,只须
恒成立,只须旧人教.files/image255.gif) ,故
,故旧人教.files/image257.gif) 又因
又因旧人教.files/image259.gif) 的最大值为7。
的最大值为7。
21.解:(Ⅰ)由已知数据,易知函数旧人教.files/image165.gif) 的周期T=12
的周期T=12
振幅A=3 b=10
旧人教.files/image262.gif)
(Ⅱ)由题意,该船进出港时,水深应不小于5+6.5=11.5(米)
旧人教.files/image264.gif)
旧人教.files/image266.gif)
解得,旧人教.files/image268.gif)
旧人教.files/image270.gif)
在同一天内,取k=0或1
旧人教.files/image272.gif) 或
或旧人教.files/image274.gif)
∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时
22.解:
(1)令旧人教.files/image276.gif)
旧人教.files/image278.gif)
在R上任取旧人教.files/image280.gif)
旧人教.files/image282.gif)
(2)要使旧人教.files/image284.gif)
旧人教.files/image286.gif)
旧人教.files/image288.gif)
法2:旧人教.files/image290.gif)
旧人教.files/image292.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com