题目列表(包括答案和解析)
最小正周期为π的函数
(其中a是小于零的常数，
是大于零的常数)的图象按向量
，(0＜θ＜π)平移后得到函数y＝f(x)的图象，而函数y＝f(x)在实数集上的值域为[－2，2]，且在区间
上是单调递减函数．
(1)求a、
和θ的值；
(2)若角α和β的终边不共线，f(α)＋g(α)＝f(β)＋g(β)，求tan(α＋β)的值．
函数
的最小正周期为
，将
的图像向左平移
个单位长度所得图像关于
轴对称，则
的一个值是（ ）
（A）
（B）
（C）
（D）
(本小题满分12分)
如下图，O1（– 2，0），O2（2，0），圆O1与圆O2的半径都是1，
(1) 过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得
．求动点P的轨迹方程；
(2) 若直线
交圆O2于A、B，又点C（3，1），当m取何值时，△ABC的面积最大？
(本小题满分15分)
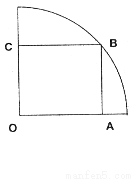
如图，在半径为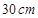
的
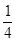圆形（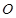
为圆心）铝皮上截取一块矩形材料
，其中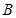点
在圆上，点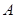
、
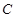在两半径上，现将此矩形铝皮卷成一个以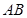
为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长
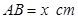，圆柱的体积为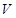
.
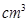（1）写出体积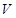关于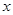
的函数关系式，并指出定义域；
（2）当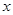为何值时，才能使做出的圆柱形罐子体积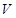最大？最大体积是多少？
(本小题满分12分)请你设计一个包装盒，如下图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上，是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(cm).
(I)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值？
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值？并求出此时包装盒的高与底面边长的比值.[
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com