
题目列表(包括答案和解析)


(14分)学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们先研究用厚度和质量分布均匀的长木条(如一把米尺)做成的摆(这种摆被称为复摆),如图 所示。让其在竖直平面内做小角度摆动,C 点为重心,木条长为 L ,周期用 T 表示 。
甲同学猜想:复摆的周期应该与木条的质量有关。
乙同学猜想:复摆的摆长应该是悬点到重心的距离 L/2 。
丙同学猜想:复摆的摆长应该大于 L/2 。理由是:若 OC 段看成细线,线栓在C处,C点以下部分的重心离O点的距离显然大于L/2。
为了研究以上猜想是否正确,同学们进行了下面的实验探索:
(1) 把两个相同的长木条完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个长木条摆动时的周期相同,重做多次仍有这样的特点。则证明了甲同学的猜想是 的(选填“正确”或“错误”) 。
(2) 用 To 表示木条长为 L 的复摆看成摆长为 L/2 单摆的周期计算值(To = 2π![]() ),用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表:
),用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表:
由上表可知,复摆的等效摆长 L/2 (选填“大于”、“小于”或“等于”) 。
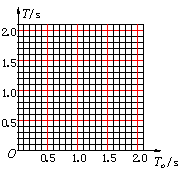
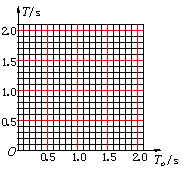
(3) 为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标
如图 13 所示。请在坐标纸上作出 T – To图线,并根据图象中反映出的规律求出
![]() /
/![]() = (结果保留三位有效数字,其中 L等 是木条长为L时的等效摆长。T = 2π
= (结果保留三位有效数字,其中 L等 是木条长为L时的等效摆长。T = 2π![]() ) 。
) 。
 |
 |
| 板长L(cm) | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值To /(s) | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/(s) | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
(14分)学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们
先研究用厚度和质量分布均匀的长木条(如一把米尺)做成的摆(这种摆被称为复摆),如图
所示。让其在竖直平面内做小角度摆动,C 点为重心,木条长为 L ,周期用 T 表示 。
甲同学猜想:复摆的周期应该与木条的质量有关。
乙同学猜想:复摆的摆长应该是悬点到重心的距离 L/2 。
丙同学猜想:复摆的摆长应该大于 L/2 。理由是:若 OC 段看成细线,线栓在C处,
C点以下部分的重心离O点的距离显然大于L/2。
为了研究以上猜想是否正确,同学们进行了下面的实验探索:
(1) 把两个相同的长木条完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个长木条摆动时的周期相同,重做多次仍有这样的特点。则证明了甲同学的猜想是 的(选填“正确”或“错误”) 。
(2) 用 To 表示木条长为 L 的复摆看成摆长为 L/2 单摆的周期计算值(To = 2π![]() ),用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表:
),用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表:
| 板长L(cm) | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值To /(s) | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/(s) | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
由上表可知,复摆的等效摆长 L/2 (选填“大于”、“小于”或“等于”) 。
(3) 为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标
如图 13 所示。请在坐标纸上作出 T – To图线,并根据图象中反映出的规律求出
![]() /
/![]() = (结果保留三位有效数字,其中 L等 是木条长为L时的等效摆长。T = 2π
= (结果保留三位有效数字,其中 L等 是木条长为L时的等效摆长。T = 2π![]() ) 。
) 。
 |
 |
在测定《梯形玻璃砖的折射率》实验中
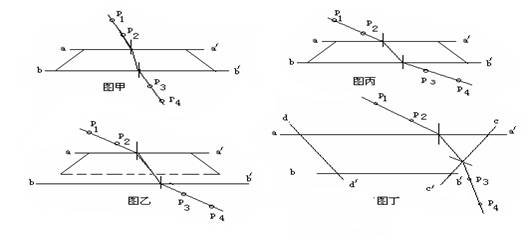
(1)四位同学分别在白纸上画出了测量梯形玻璃砖折射率的光路图,光路图如图甲、乙、丙、丁所示,直线aa/、bb/、cc/、dd/代表梯形玻璃砖在白纸上的界面。其中p1、p2、p3、p4为4枚大头针所插位置的投影点,光线的箭头没有画出。能比较准确测量折射率的光路图可以是
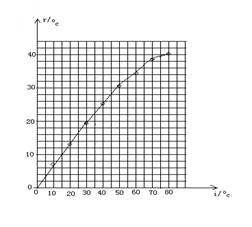
(2)为了探究折射角(r)与入射角(i)的关系,已作 出折射角随入射角的变化曲线,如图所示,请指出图线的特征 。
你猜想一下,入射角与折射角 之比 是一个常数。(猜对给分,猜不对不给分)
在测定《梯形玻璃砖的折射率》实验中
(1)四位同学分别在白纸上画出了测量梯形玻璃砖折射率的光路图,光路图如图甲、乙、丙、丁所示,直线aa/、bb/、cc/、dd/代表梯形玻璃砖在白纸上的界面。其中p1、p2、p3、p4为4枚大头针所插位置的投影点,光线的箭头没有画出。能比较准确测量折射率的光路图可以是
(2)为了探究折射角(r)与入射角(i)的关系,已作 出折射角随入射角的变化曲线,如图所示,请指出图线的特征 。
你猜想一下,入射角与折射角 之比 是一个常数。(猜对给分,猜不对不给分)
1.A 2.D 3.B 4.AC 5.B 6.B 7.B 8.AC 9.ABD 10.BD
11.⑴①③②④ (2分)
⑵D (2分)
⑶ 是n个点对应的圆心角,t是打点计时器的打点时间间隔 (2分)
是n个点对应的圆心角,t是打点计时器的打点时间间隔 (2分)
⑷没有影响 (1分)
12.⑴乙同学的猜想是对的,当新弹簧所受拉力为F时,其中A弹簧的伸长量 ,B弹簧的伸长量
,B弹簧的伸长量 ,而
,而 ,可得
,可得 (3分)
(3分)
⑵铁架台,刻度尺 (2分)
⑶①将新弹簧悬挂在铁架台上,用刻度尺测出弹簧的长度
②在弹簧下端挂上n个钩码,测出此时弹簧的长度
③将测量结果代入 得到
得到 的值
的值
④改变n的值,多测几次,取 的平均值代入
的平均值代入 进行验证 (3分)
进行验证 (3分)
13.解:设轨道ab与水平面间的夹角为θ,由几何关系可知:
 轨道ab的长度
轨道ab的长度 (3分)
(3分)
由牛顿第二定律可得,小球下滑的加速度 (2分)
(2分)
由运动学公式得  (2分)
(2分)
联立以上各式解得  (2分)
(2分)
14.解:⑴设中央恒星O的质量为M,A行星的质量为m,则由万有引力定律和牛顿第二定律得  (3分)
(3分)
解得  (1分)
(1分)
⑵由题意可知:A、B相距最近时,B对A的影响最大,且每隔 时间相距最近,设B行星的周期为
时间相距最近,设B行星的周期为 ,则有
,则有  (1分)
(1分)
解得  (1分)
(1分)
设B行星的运行轨道半径为 ,根据开普勒第三定律有
,根据开普勒第三定律有  (2分)
(2分)
解得  (1分)
(1分)
15.解:⑴被困人员在水平方向上做匀速直线运动,在竖直方向上被困人员的位移
 ,由此可知,被困人员在竖直方向上做初速度为零、加速度
,由此可知,被困人员在竖直方向上做初速度为零、加速度 的匀加速直线运动 (2分)
的匀加速直线运动 (2分)
由牛顿第二定律可得  (1分 )
(1分 )
解得悬索的拉力  (1分)
(1分)
⑵被困人员5s末在竖直方向上的速度为  (1分)
(1分)
合速度  (1分)
(1分)

解得  (2分)
(2分)
16.⑴米袋在AB上加速时的加速度 (1分)
(1分)
米袋的速度达到 时,滑行的距离
时,滑行的距离 ,因此米袋在到达B点之前就有了与传送带相同的速度 (2分)
,因此米袋在到达B点之前就有了与传送带相同的速度 (2分)
设米袋在CD上运动的加速度大小为a,由牛顿第二定律得
 (1分)
(1分)
代入数据得  (1分)
(1分)
所以能滑上的最大距离  (1分)
(1分)
⑵设CD部分运转速度为 时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为
时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为 之前的加速度为
之前的加速度为
 (1分)
(1分)
米袋速度小于 至减为零前的加速度为
至减为零前的加速度为
 (1分)
(1分)
由 (2分)
(2分)
解得  ,即要把米袋送到D点,CD部分的速度
,即要把米袋送到D点,CD部分的速度 (1分)
(1分)
米袋恰能运到D点所用时间最长为  (1分)
(1分)
若CD部分传送带的速度较大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,则所用时间最短,此种情况米袋加速度一直为 。
。
由 (1分)
(1分)
所以,所求的时间t的范围为  (1分)
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com