∴CC1⊥AC，
∵BC=CC1，
∴BCC1B1为正方形。
∴BC1⊥B1C…………………………2分
又∵∠ACB=90°，
∴AC⊥BC
∴AC⊥平面BCC1B1，
∵B1C为AB1在平面BCC1B1内的射影，BC1⊥B1C，
∴AB1⊥BC1，………………………………4分
（2）解：
∵BC//B1C，
∴BC//平面AB1C1，
∴点B到平面AB1C1的距离等于点C到平面AB1C1的距离 ………………5分
连结A1C交AC1于H，
∵ACC1A1是正方形，
∴CH⊥AC1。
∵B1C1⊥A1C1，B1C1⊥CC1，
∴B1C1⊥A1C1，B1C1⊥CC1，
∴B1C1⊥平面ACC1A1。
∴B1C1⊥CH。
∴CH⊥平面AB1C1，
∴CH的长度为点C到平面AB1C1的距离。
∵
∴点B到平面AB1C1的距离等于
…………………………8分
（3）取A1B1的中点D，连接C1D，
∵△A1B1C1是等腰三角形，所以C1D⊥A1B1，
又∵直三棱柱ABC―A1B1C1中，侧面A1B1BA⊥底面A1B1C1，
∴C1D⊥侧面A1B1BA。
作DE⊥AB1于E，；连C1E，则DE为C1E的平面A1B1BA内的射影，
∴C1E⊥AB1
∴∠C1ED为二面角C1―AB1―A1的平面角。……………………10分
由已知C1D=
∴
∴
即二面角C1―AB1―A1的大小为60°…………………………12分
解法二：
如图建立直角坐标系，其为C为坐标原点，依题意A（2，0，0），B（0，2，0），A1（2，0，2），B1（0，2，2），C1（0，0，2）。…………………………2分
（1）证明：
 …………………………4分
（2）解： 设 的法向量， 由 得 
令 ………………………………6分  ，
∴点B到平面AB1C1的距离 ……………………8分 （3）解设 是平面A1AB1的法向量 由 
令 …………………………10分 
∴二面角C1―AB―A1的大小为60°。…………………………12分 20．（本小题满分12分） （1）解：由已知得切点A的坐标为 …………2分 
即 由 ……………………5分 （2）证明：由（1）得 它的定义域为 ， 
 上是增函数。
 是增函数，……………………9分
 ………………………………12分
21．（本小题满分12分）
（1）解：设椭圆E的方程为 …………2分 设 
 为直角三角形，且 ，
又 
又为直角三角形，且 ， 
 
 ……………………4分
∴椭圆E的方程为 …………………………6分
（2）椭圆E的左准线方程为 由 ∴线段PQ的中点M的横坐标为  …………………………9分
（3）解：  点Q分有向线段 ，
 是以 为自变量的增函数，
 …………………………12分
22．（本小题满分12分）
（1）当x=y=0时， 解得 ……………………1分 当x=1， 时， 
 ……………………3分
（2）解：当x是正整数，y=1时，由已知得 
 …………………………5分
当x是负整数时，取 ， 则是正整数 
 .
又  ……………………7分
它所有的整数解为―3，―1，1，3. 它们能构成的两个等差数列，即数列―3，―1，1，3以及数列3，1，―1，―3…12分 请注意：以上参考答案与评分标准仅供阅卷时参考，其他答案请参考评分标准酌情给分。
| |
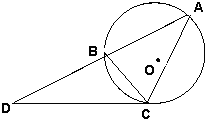（1）圆O是△ABC的外接圆，过点C的圆的切线与AB的延长线交于点D，CD=2
（1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．
15．4 16．
2分
5分
7分
，
10分
，
表示一天之内需要调整的部件数，则
……3分
……………………12分