
题目列表(包括答案和解析)
如图,D,E分别是△ABC边AB,AC的中点,直线DE交△ABC的外接圆与F,G两点,若CF∥AB,证明:

(Ⅰ) CD=BC;
(Ⅱ)△BCD∽△GBD.
【命题意图】本题主要考查线线平行判定、三角形相似的判定等基础知识,是简单题.
【解析】(Ⅰ) ∵D,E分别为AB,AC的中点,∴DE∥BC,
∵CF∥AB, ∴BCFD是平行四边形,
∴CF=BD=AD, 连结AF,∴ADCF是平行四边形,

∴CD=AF,
∵CF∥AB, ∴BC=AF, ∴CD=BC;
(Ⅱ) ∵FG∥BC,∴GB=CF,
由(Ⅰ)可知BD=CF,∴GB=BD,
∵∠DGB=∠EFC=∠DBC, ∴△BCD∽△GBD
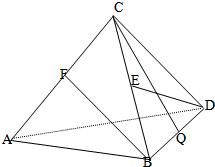 四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.
四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.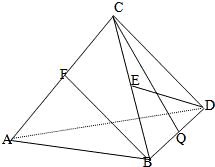 四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.
四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。
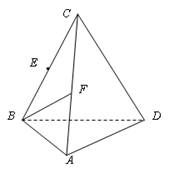
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在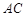 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com