
题目列表(包括答案和解析)
已知命题p:关于![]() 的方程
的方程![]() 有两不等实根;命题q:关于
有两不等实根;命题q:关于![]() 的不等式
的不等式![]()
![]() 的解集为R.
的解集为R.
(1)若p为真命题且q为假命题,试求![]() 的取值范围;w.w.w.k.s.5.u.c.o.m
的取值范围;w.w.w.k.s.5.u.c.o.m ![]()
![]()
已知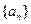 为等比数列,
为等比数列,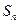 是它的前
是它的前 项和.若
项和.若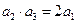 , 且
, 且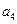 与2
与2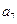 的等差中项为
的等差中项为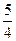 ,则
,则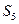 =" " ( )w_w w.k*s_5 u.c o_m
=" " ( )w_w w.k*s_5 u.c o_m
| A.35 | B.33 | C.31 | D.29 |
已知二面角![]() 的大小为
的大小为![]() ,
,![]() 为空间中任意一点,则过点
为空间中任意一点,则过点![]() 且与平面
且与平面![]() 和平面
和平面![]() 所成的角都是
所成的角都是![]() 的直线的条数为( )w.w.w.k.s.5.u.c.o.m
的直线的条数为( )w.w.w.k.s.5.u.c.o.m ![]()
![]()
A.2 B.3 C.4 D.5 w.w.w.k.s.5.u.c.o.m ![]()
![]()
定义在R上的函数f (x)满足:如果对任意x1,x2![]() R,都有
R,都有![]() ,则称函数f (x)是R上的凹函数.已知二次函数
,则称函数f (x)是R上的凹函数.已知二次函数![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m ![]()
(1)当![]() 时,试判断函数f (x)是否为凹函数,并说明理由;
时,试判断函数f (x)是否为凹函数,并说明理由;
(2)如果函数f (x)对任意的x![]() [0,1]时,都有
[0,1]时,都有![]() ,试求实数a的范围。
,试求实数a的范围。
已知点P是抛物线![]() 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
A
A
B
B
B
C
C
A
11. -3 12. 3 13. /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image275.gif) 14.
14./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image277.gif)
15. 4 (5,1,3)
16.⑴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image279.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image281.gif)
⑵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image283.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image285.gif)
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image287.gif)
由于/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image285.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image289.gif)
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image291.gif) 时
时 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image293.gif)
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image295.gif) 时
时 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image297.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image299.gif)
此时/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image301.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image303.gif)
综上/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image299.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image158.gif) 取最大值
取最大值/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image182.gif) 时,
时, /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image303.gif)
17.⑴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image308.gif)
因为函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image188.gif) 的图象在点
的图象在点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image190.gif) 处的切线与直线
处的切线与直线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image193.gif) 平行,所以
平行,所以/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image313.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image315.gif) 。
(文2分)
。
(文2分)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image188.gif) 过点
过点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image190.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image317.gif) (文4分,理3分)
(文4分,理3分)
⑵由⑴知,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image319.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image321.gif) 。
。
令/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image323.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image325.gif) 或
或/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image327.gif) ,
,
易知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image158.gif) 的单调递增区间为
的单调递增区间为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image330.gif) ,单调递减区间为
,单调递减区间为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image332.gif) 。
。
(文6分,理5分)。
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif) 当
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image336.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image158.gif) 的最大值为
的最大值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image339.gif) ,最小值为
,最小值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image341.gif) ;
;
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image343.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image158.gif) 的最大值为
的最大值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image339.gif) ,最小值为
,最小值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image346.gif) ; (文10分,理7分)
; (文10分,理7分)
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image348.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image158.gif) 的最大值为
的最大值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image351.gif) ,最小值为
,最小值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image346.gif) ; (文12分,理8分)
; (文12分,理8分)
⑶因为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image354.gif) 为连续函数,所以
为连续函数,所以/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image356.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image358.gif)
由⑵得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image360.gif) ,则
,则
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image362.gif) ,(理10分)
,(理10分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image364.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image366.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image368.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image370.gif) 。 (理12分)
。 (理12分)
18.⑴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image372.gif) ,且平面
,且平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image211.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image062.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image376.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image378.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image380.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image378.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image384.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image386.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image389.gif) 为二面角
为二面角/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image391.gif) 的平面角。 (4分)
的平面角。 (4分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image393.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image395.gif) J是等边三角形,
J是等边三角形,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image398.gif) ,即二面角
,即二面角/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image391.gif) 的大小为
的大小为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image400.gif) 。 (5分)
。 (5分)
⑵(理)设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image402.gif) 的中点为
的中点为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image404.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image406.gif) 的中点为
的中点为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image408.gif) ,连结
,连结/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image410.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image412.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image414.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image416.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image418.gif) ,①
,①
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image421.gif) ,且平面
,且平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image211.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image062.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image426.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image378.gif) 。 (7分)
。 (7分)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image429.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image378.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image433.gif) 。
②
。
②
由①、②知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image435.gif)
由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image437.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image439.gif) ,得四边形
,得四边形/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image441.gif) 为平行四边形,
为平行四边形,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image444.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image447.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image218.gif) ,又
,又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image393.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image451.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image453.gif) ,
,
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image216.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image218.gif) 。
。
19.⑴三人恰好买到同一只股票的概率/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image457.gif) 。 (文4分,理3分)
。 (文4分,理3分)
⑵解法一 三人中恰好有两个买到同一只股票的概率/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image459.gif) 。 (文9分,理7分)
。 (文9分,理7分)
由⑴知,三人恰好买到同一只股票的概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image461.gif) ,所以三人中至少有两人买到同一只股票的概率
,所以三人中至少有两人买到同一只股票的概率/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image463.gif) 。 (文12分,理9分)
。 (文12分,理9分)
解法二 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image465.gif) 。 (文12分,理9分)
。 (文12分,理9分)
⑶(只理科做)每股今天获利钱数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image467.gif) 的分布列为:
的分布列为:
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image467.gif)
2
0
-1
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image064.gif)
0.5
0.2
0.3
所以,1000股在今日交易中获利钱数的数学期望为
1000/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image470.gif) (理12分)
(理12分)
20.⑴由题意可知,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image472.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image474.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image476.gif) ,
,
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image478.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image480.gif) (3分)
(3分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image482.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif) 顶点
顶点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image245.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image247.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image249.gif) 不在同一条直线上。 (4分)
不在同一条直线上。 (4分)
⑵由题意可知,顶点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image251.gif) 横、纵坐标分别是
横、纵坐标分别是/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image489.gif) 。
。
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image491.gif) ,
,
消去/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image493.gif) ,可得
,可得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image495.gif) 。 (12分)
。 (12分)
为使得所有顶点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image251.gif) 均落在抛物线
均落在抛物线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image497.gif) 上,则有
上,则有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image499.gif) 解之,得
解之,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image501.gif) (14分)
(14分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image106.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image235.gif) 所以应满足的关系式是:
所以应满足的关系式是:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image506.gif) 。 (16分)
。 (16分)
解法二 点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image508.gif) 的坐标满足
的坐标满足/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image510.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image393.gif) 点
点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image508.gif) 在抛物线
在抛物线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image513.gif) 上,
上,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image515.gif)
又点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image517.gif) 的坐标满足
的坐标满足/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image519.gif) 且点
且点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image517.gif) 也在抛物线上,
也在抛物线上,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image393.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image522.gif) 把点
把点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image517.gif) 代入抛物线方程,解得
代入抛物线方程,解得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image506.gif) 。(13分)
。(13分)
因此,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image525.gif) ,抛物线方程为
,抛物线方程为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image527.gif) 。
。
又 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image529.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif) 所有顶点
所有顶点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image532.gif) 均落在抛物线
均落在抛物线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image527.gif) 上
上
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image334.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image106.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image235.gif) 所应满足的关系式是:
所应满足的关系式是:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image538.gif) 。
。
21.⑴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image540.gif) ,
,
由题意,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image542.gif) , (2分)
, (2分)
⑵由⑴,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(3).files\image544.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com