
题目列表(包括答案和解析)
已知函数![]() 图像上的点
图像上的点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若函数![]() 在
在![]() 时有极值,求
时有极值,求![]() 的表达式
的表达式
(2)函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围
的取值范围
已知函数 图像上的点
图像上的点 处的切线方程为
处的切线方程为 .
.
(1)若函数 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
((12分)已知函数 图像上的点
图像上的点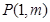 处的切线方程为
处的切线方程为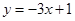 .[来
.[来
(1)若函数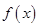 在
在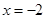 时有极值,求
时有极值,求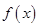 的表达式;
的表达式;
(2)函数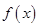 在区间
在区间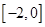 上单调递增,求实数
上单调递增,求实数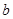 的取值范围。
的取值范围。
已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ)函数![]() 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用![]() 表示);
表示);
(Ⅱ)若![]() 不是函数
不是函数![]() 的极值点,求证:函数
的极值点,求证:函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.
已知函数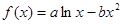 图像上一点
图像上一点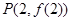 处的切线方程为
处的切线方程为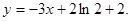 (1)求
(1)求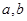 的值;(2)若方程
的值;(2)若方程 在区间
在区间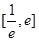 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令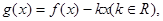 如果
如果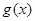 的图像与
的图像与 轴交于
轴交于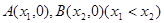 两点,
两点,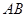 的中点为
的中点为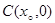 ,求证:
,求证: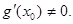
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
C
C
B
D
B
A
D
A
C
D
D
二、填空题
13、45 14、 15、
15、 16、0.94 17、
16、0.94 17、 18、
18、
三、解答题
19、解: f(x)=
f(x)= ?(
?( -1)
-1) 

 f(x)=
f(x)= (2x+1)=2?0+1=1
(2x+1)=2?0+1=1
∴
20、解:(1)当a=2时,A=(2,7),B=(4,5)∴ A B=(4,5)
B=(4,5)
(2)∵ B=(
当a< 时,A=(
时,A=( A,必须
A,必须 ,此时a=-1;
,此时a=-1;
当a= 时,A=
时,A= ,使B
,使B A的a不存在;
A的a不存在;
当a> 时,A=(2,
时,A=(2, A,必须
A,必须 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}
21、解:(1)ξ可能的取值为0,1,2,3.
P(ξ=0)=?== P(ξ=1)=?+?=
P(ξ=2)=?+?= P(ξ=3)=?=.
ξ的分布列为
ξ
0
1
2
3
P
数学期望为Eξ=1.2.
(2)所求的概率为
p=P(ξ≥2)=P(ξ=2)+P(ξ=3)=+=
22、解: ,(2分)
,(2分)
因为函数 在
在 处的切线斜率为-3,
处的切线斜率为-3,
所以 ,即
,即 ,
1
,
1
又 得
得 。
2
。
2
(1)函数 在
在 时有极值,所以
时有极值,所以 , 3
, 3
解123得 ,
,
所以 .
.
(2)因为函数 在区间
在区间 上单调递增,所以导函数
上单调递增,所以导函数 在区间
在区间 上的值恒大于或等于零,
上的值恒大于或等于零,
则 得
得 ,所以实数
,所以实数 的取值范围为
的取值范围为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com