
题目列表(包括答案和解析)
(本题满分16分)
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数。
的生成函数。
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由。
的生成函数?并说明理由。
第一组:![]() ;
;
第二组:![]() 。
。
(2)设![]() ,生成函数
,生成函数![]() 。若不等式
。若不等式![]()
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围。
的取值范围。
(3)设![]() ,取
,取![]() 生成函数
生成函数![]() 图象的最低点坐标为
图象的最低点坐标为![]() 。
。
若对于任意正实数![]() 且
且![]() ,
,
试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
(本小题满分14分)
已知函数![]() 对于任意
对于任意![]() (
(![]() ),都有式子
),都有式子![]() 成立(其中
成立(其中![]() 为常数).
为常数).
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)利用函数![]() 构造一个数列,方法如下:
构造一个数列,方法如下:
对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述构造过程中,如果![]() (
(![]() =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果![]() 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求![]() 的取值范围;
的取值范围;
(ⅱ)是否存在一个实数![]() ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为![]() ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(ⅲ)当![]() 时,若
时,若![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(本小题满分13分)
设函数 对任意的实数
对任意的实数 ,都有
,都有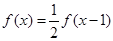 ,且当
,且当 时,
时, 。
。
(1)若 时,求
时,求 的解析式;
的解析式;
(2)对于函数 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点 ,使得函数在点
,使得函数在点 处的切线与
处的切线与 平行。若存在,那么这样的点
平行。若存在,那么这样的点 有几个;若不存在,说明理由。
有几个;若不存在,说明理由。
(3)已知 ,且
,且  ,记
,记 ,求证:
,求证:  。
。
(本小题共13分)
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表:
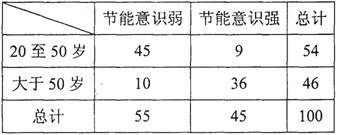
(1)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(2)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(3)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率。
(本小题满分12分)(注意:在试题卷上作答无效)
函数 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若函数 的图象与
的图象与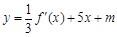 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在点P,使得过点P的直线若能与曲线 围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com