
题目列表(包括答案和解析)
| a |
| a |
| b |
| aibi | ||
|
| a |
| b |
A、-
| ||
| B、1 | ||
| C、2 | ||
D、
|
| a |
| b |
| a |
| b |
| ||||||||||||
|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| ||||||||||||
|
| a |
| b |
| a |
| b |
| n-4 |
| n |
| n-4 |
| n |
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量 ,
, ,当
,当 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到 维向量,n维向量可用
维向量,n维向量可用 规定向量
规定向量
 = ( )
= ( )
A.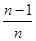 B.
B. C.
C. D.
D.
1、C 2、A 3、C 4、A 5、C 6、B 7、B 8、D 9、A 10、C 11、B 12、D
13、1.56 14、5 15、
.files/image226.gif)
16、(1)斜面的中面面积等于斜面面积的四分之一;(2)三个直角面面积的平方和等于斜面面积的平方;(3)斜面与三个直角面所成二面角的余弦平方和等于1,等等
17、解:
(Ⅰ).files/image138.gif) =
=.files/image227.gif)
=.files/image228.gif) =
=.files/image229.gif) =
= .files/image230.gif)
(Ⅱ) ∵ .files/image231.gif) ∴
∴ .files/image232.gif) ,
,
又∵ .files/image139.gif) ∴
∴ .files/image233.gif) 当且仅当 b=c=
当且仅当 b=c=.files/image234.gif) 时,bc=
时,bc=.files/image235.gif) ,故bc的最大值是
,故bc的最大值是.files/image235.gif) .
.
18、.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image251.gif)
19、(1)证明:.files/image253.gif)
.files/image152.gif) 底面
底面.files/image154.gif)
.files/image255.gif)
且.files/image257.gif)
.files/image259.gif)
.files/image261.gif)
.files/image259.gif) 平面
平面.files/image160.gif) 平面
平面.files/image162.gif)
(2)解:因为.files/image264.gif) ,且
,且.files/image266.gif) ,
,
可求得点.files/image168.gif) 到平面
到平面.files/image170.gif) 的距离为
的距离为.files/image268.gif)
(3)解:作.files/image270.gif) ,连
,连.files/image272.gif) ,则
,则.files/image274.gif) 为二面角
为二面角.files/image176.gif) 的平面角
的平面角
设.files/image276.gif) ,
,.files/image278.gif) ,在
,在.files/image280.gif) 中,求得
中,求得.files/image282.gif) ,
,
同理,.files/image284.gif) ,由余弦定理
,由余弦定理.files/image286.gif)
解得.files/image288.gif) , 即
, 即.files/image174.gif) =1时,二面角
=1时,二面角.files/image176.gif) 的大小为
的大小为.files/image178.gif)
20、
.files/image290.jpg) 21、解:设
21、解:设.files/image292.gif)
由题意可得:.files/image294.gif)
即.files/image296.gif)
又.files/image298.gif)
相减得:.files/image300.gif)
∴.files/image302.gif)
∴直线.files/image201.gif) 的方程为
的方程为.files/image304.gif) ,即
,即.files/image306.gif) .
.
(2)设.files/image203.gif) :
:.files/image308.gif) ,代入圆的方程整理得:
,代入圆的方程整理得:
.files/image310.gif)
∵.files/image312.gif) 是上述方程的两根
是上述方程的两根
∴.files/image314.gif)
同理可得:.files/image316.gif)
∴.files/image318.gif) .
.
22、解:(1)由题意,.files/image218.gif) 在[
在[.files/image210.gif) ]上递减,则
]上递减,则.files/image320.gif) 解得
解得.files/image322.gif)
所以,所求的区间为[-1,1]
取.files/image331.gif)
.files/image333.gif) ,
,
即.files/image023.gif) 不是
不是.files/image329.gif) 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数.files/image216.gif)
(3)若.files/image222.gif) 是闭函数,则存在区间[
是闭函数,则存在区间[.files/image210.gif) ],在区间[
],在区间[.files/image210.gif) ]上,函数
]上,函数.files/image023.gif) 的值域为[
的值域为[.files/image210.gif) ],即
],即.files/image335.gif) ,
,.files/image337.gif) 为方程
为方程.files/image339.gif) 的两个实数根,
的两个实数根,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com