
题目列表(包括答案和解析)
若 的图象关于点M(
的图象关于点M(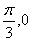 )对称,且在
)对称,且在 处函数有最小值,则
处函数有最小值,则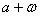 的一个可能的取值是 ( )
的一个可能的取值是 ( )
A.0 B.3 C.6 D.12
小明家中有两种酒杯,一种酒杯的轴截面是等腰直角三角形,称之为直角酒杯(如图1),另一种酒杯的轴截面近似一条抛物线,杯口宽4 cm,杯深为8 cm(如图2),称之为抛物线酒杯.

(1)请选择适当的坐标系,求出抛物线酒杯的方程.
(2)一次,小明在游戏中注意到一个现象,若将一些大小不等的玻璃球依次放入直角酒杯中,则任何玻璃球能触及酒杯杯底.但若将这些玻璃球放入抛物线酒杯中,则有些小玻璃不能触及酒杯杯底.小明想用所学过数学知识研究一下,当玻璃球的半径r为多大值时,玻璃球一定会触及酒杯杯底部.你能帮助小明解决这个问题吗?
(3)在抛物线酒杯中,放入一根粗细均匀,长度为2 cm的细棒,假设细棒的端点与酒杯壁之间的摩擦可以忽略不计,那么当细棒最后达到平衡状态时,细棒在酒杯中位置如何?
(08年金华一中) 若![]() 的图象关于点
的图象关于点![]() 对称,且在
对称,且在![]() 处函数有最小值,则
处函数有最小值,则![]() 的一个可能的取值是( )
的一个可能的取值是( )
A.0 B
函数![]() 的导函数
的导函数![]() 的图像如右图,则
的图像如右图,则![]() 的图象最有可能是( )
的图象最有可能是( )
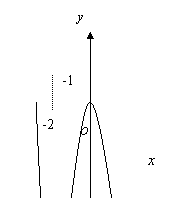
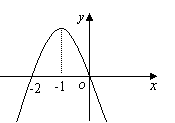
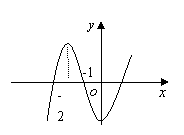

(A) (B)
 |  | ||
(C) (D)
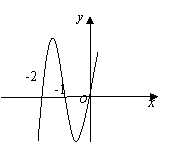
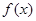 的导函数
的导函数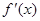 的图象如图所示,则函数
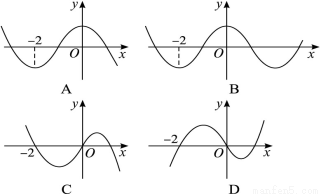
的图象如图所示,则函数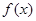 的图象最有可能是下图中的
的图象最有可能是下图中的

一.选择题 1B 2B 3B
二.填空题 13.3 14.  15.
15.  16.
16. 
三.解答题
17.解:由已知 所以
所以
所以 .…… 4分
.…… 4分
由 解得
解得 .
.
所以 …… 8分
…… 8分
于是 …… 10分
…… 10分
故 …… 12分
…… 12分
18.(Ⅰ)设{an}的公比为q,由a3=a1q2得  …… 2分
…… 2分
 (Ⅱ)
(Ⅱ) …… 12分
…… 12分
19.解: (1)由 知,
知,  …① ∴
…① ∴ …②…… 2分
…②…… 2分
又 恒成立,
恒成立,
有 恒成立, 故
恒成立, 故 …… 4分
…… 4分
将①式代入上式得:
 , 即
, 即 故
故 , 即
, 即 ,代入②得,
,代入②得, …… 8分
…… 8分
(2)
 即
即 ∴
∴ 解得:
解得:
 , ∴不等式的解集为
, ∴不等式的解集为 …… 12分
…… 12分
20、证(I)由a1=1,an+1= Sn(n=1,2,3,…),知a2=
Sn(n=1,2,3,…),知a2= S1=
S1= ,
,  ,∴
,∴
又an+1=Sn+1-Sn(n=1,2,3,…),则Sn+1-Sn= Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
 (n=1,2,3,…).故数列{
(n=1,2,3,…).故数列{ }是首项为1,公比为2的等比数列
}是首项为1,公比为2的等比数列  …… 8分
…… 8分
证(II) 由(I)知, ,于是Sn+1=4(n+1)?
,于是Sn+1=4(n+1)? =4an(n
=4an(n )…… 12分
)…… 12分
又a2=3S1=3,则S2=a1+a2=4=
21. 解:(1) .
.
 …… 2分
…… 2分
当 时,
时,
 时,
时, , 因此
, 因此 的减区间是
的减区间是

 在区间
在区间 上是减函数
上是减函数 …… 5分
…… 5分
当 时,
时,
 时,
时, , 因此
, 因此 的减区间是
的减区间是 …… 7分
…… 7分

 在区间
在区间 上是减函数
上是减函数
综上, 或
或 …… 8分
…… 8分
(2). 若



 在区间
在区间 上,
上,  …… 12分
…… 12分
22.解:(1)由题意和导数的几何意义得:

由(1)得c=-a
 …… 6分
…… 6分

 …… 10分
…… 10分
 …… 14分
…… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com