题目列表(包括答案和解析)
记数列{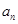
}的前n项和为为
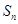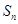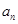，且＋＋n＝0（n∈N*）恒成立．
（1）求证：数列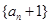
是等比数列；
（2）已知2是函数f（x）＝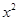
＋ax－1的零点，若关于x的不等式f（x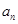）≥对任意n∈N﹡在x∈（－∞，λ]上恒成立，求实常数λ的取值范围．
记数列{
}的前n项和为为
，且＋＋n＝0（n∈N*）恒成立．
（1）求证：数列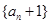
是等比数列；
（2）已知2是函数f（x）＝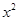
＋ax－1的零点，若关于x的不等式f（x）≥对任意n∈N﹡在x∈（－∞，λ]上恒成立，求实常数λ的取值范围．
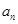}的前n项和为为
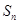，且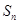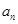＋＋n＝0（n∈N*）恒成立．
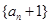是等比数列；
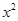＋ax－1的零点，若关于x的不等式f（x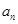）≥对任意n∈N﹡在x∈（－∞，λ]上恒成立，求实常数λ的取值范围．已知函数f（x）=x2－4，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n
），其中
为正实数.
（Ⅰ）用
表示xn+1；
（Ⅱ）若a1=4，记an=lg
，证明数列｛
｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若x1＝4，bn＝xn－2，Tn是数列｛bn｝的前n项和，证明Tn<3.
已知等差数列{an}的公差大于0，且a3，a5是方程x2－14x＋45＝0的两根，数列{bn}的前n项和为Sn，且Sn＝1－ bn.
(1)求数列{an}、{bn}的通项公式；
(2)记cn＝anbn，求证：cn＋1≤cn.
一．选择题 1B 2B 3B
二.填空题 13.3 14. 
15. 
16. 
三.解答题
17.解：由已知
所以
所以
.…… 4分
由
解得
.
所以
…… 8分
于是
…… 10分
故
…… 12分
18.（Ⅰ）设{an}的公比为q，由a3=a1q2得 
…… 2分
（Ⅱ）
…… 12分
19．解: (1)由
知, 
…① ∴
…②…… 2分
又
恒成立,
有
恒成立, 故
…… 4分
将①式代入上式得:
, 即
故
, 即
,代入②得,
…… 8分
(2)
即
∴
解得:
, ∴不等式的解集为
…… 12分
20、证（I）由a1=1,an+1=
Sn(n=1,2,3，…)，知a2=
S1=
, 
,∴
又an+1=Sn+1-Sn(n=1,2,3，…),则Sn+1-Sn=Sn(n=1,2,3，…)，∴nSn+1=2(n+1)Sn,
(n=1,2,3，…).故数列{
}是首项为1，公比为2的等比数列 
…… 8分
证（II） 由（I）知，
，于是Sn+1=4(n+1)?
=4an(n
)…… 12分
又a2=3S1=3,则S2=a1+a2=4=
21. 解:(1)
.
…… 2分
当
时,
时,
, 因此
的减区间是
在区间
上是减函数
…… 5分
当
时,
时,, 因此的减区间是
…… 7分
在区间上是减函数
综上,
或
…… 8分
(2). 若
在区间
上, 
…… 12分
22.解：（1）由题意和导数的几何意义得：
由（1）得c=-a
…… 6分
…… 10分
…… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com