练习册

  • 练习册
  • 试题
    22(本小题满分12分)定义在R上的函数满足且对任意.都有. 【查看更多】

     

    题目列表(包括答案和解析)

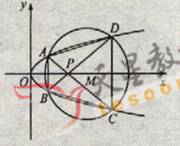    (22) （本小题满分12分）（注意：在试题卷上作答无效）如图，已知抛物线与圆相交于A、B、C、D四个点。

    （Ⅰ）求r的取值范围

    （Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标。

    查看答案和解析>>

    （

    请考生在第22~23两题中任选一题做答，如果多做，则按所做的第一题记分。

    22．(本小题满分12分)

    已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．

    （1）求f(x)的解析式；

    （2）求函数g(x)=f(x2)的单调递增区间.

     

    查看答案和解析>>

    (本小题满分12分)

    已知函数,且.

    （Ⅰ）求的定义域；

    （Ⅱ）判断的奇偶性并予以证明；

    （Ⅲ）当时，求使的的取值范围.

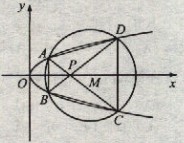
    （22）(本小题满分12分)

    已知为圆上任一点，且点．

        （Ⅰ）若在圆上，求线段的长及直线的斜率；

    （Ⅱ）求的最大值和最小值．

    查看答案和解析>>

    (本小题满分12分)

    某中学高三文科共有四个班，第二次月考后，随机在各班抽取了部分学生的数学成绩进行统计分析.已知各班被抽取的学生人数恰好成等差数列，且人数最少的班被抽取了22人. 从四个班抽取出来的所有学生的数学成绩的频率分布直方图如图所示，其中共有5人的成绩在120～130分(含120分但不含130分).

         （Ⅰ）求各班被抽取的学生人数各为多少人？

    （Ⅱ）在被抽取的所有学生中任选一人，

    求该生的数学成绩不小于90分的概率.

    查看答案和解析>>

    （（本小题满分12分）

        编号分别为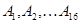的16名篮球运动员在某次比赛中得分记录如下；

    编号

    A1

    A2

    A3

    A4

    A5

    A6

    A7

    A8

    得分

    15

    35

    21

    28

    25

    36

    18

    34

    编号

    A9

    A10

    A11

    A12

    A13

    A14

    A15

    A16

    得分

    17

    26

    25

    33

    22

    12

    31

    38

    （Ⅰ）将得分在对应区间的人数填入相应的空格内：

    区   间

    人   数

     

     

     

    （Ⅱ）从得分在区间内的运动员中随机抽取2人.

    (1)用运动员编号列出所有可能的抽取结果；

    (2)求这两人得分之和大于50的概率.

     

     

    查看答案和解析>>

    Ⅰ 选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    D

    A

     B

    C

    C

    B

    C

    C

    B

    A

    A

    B

     

    Ⅱ 非选择题

    二、13．         14．4          15．-2            16．①  ②   

    三、解答题：

    17．（I）解：

        --------------------------4分

    当，即时，取得最大值.

    因此，取得最大值的自变量x的集合是  -------8分

    （Ⅱ）解：

    由题意得，即.

    因此，的单调增区间是.-------------------13分

    18．⑴∵f (x) ≥x的解集为R

    ∴x2－（4a＋1）x＋a2≥0对于x∈R恒成立        -----------------------------------2分

    ∴△＝（4a＋1）2－4a2≤0

      即12 a2＋8a＋1≤0             --------------------------------------------------------4分

        （2a＋1）（6a＋1）≤0

    ∴?≤a≤?

    ∴a的取值范围为[?，?]       ------------------------------------------------------6分

    （2）∵，---------------------------------------------------------8分

    由的对称轴，知在单调递增

    ∴在处取得最小值，即---------------------------------------------------11分

    ∴    解得或  ∵        ∴----------------------13分

    19、解：由<0,得

    即(*)----------------------------------------------------------------------2分

    ⑴当 a＞0时，（*）等价于＜0  a＞0时，

    ∴不等式的解为：＜x＜1--------------------------------------------------------------------5分   

    ⑵当a=0时，（*）等价于＜0即x＜1----------------------------------------------------8分

    ⑶当a＜0时，（*）等价于＞0  a＜0时，

    ∴   不等式的解为 ： x＜1或x＞-----------------------------------------------------11分

    综上所述：当a＞0时，不等式的解集为（，1）；当a=0时，不等式的解集为；

    当a＜0时，不等式的解集为∪（，）-------------------------------12分

    20．

    ---------------------------------------------------------------------------------3分

    ---------------------------------------------------------------------7分

    ---------------------------------12分

    21．解：(1)由已知

    　　，

     

    (2)

    　椭圆的方程为

    22．(1)证明：f(x+y)=f(x)+f(y)(x，y∈R)，　　　　　　　　　　　　 ①

    令x=y=0，代入①式，得f(0+0)=f(0)+f(0)，即 f(0)=0．

    令y=-x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，则有0=f(x)+f(-x)．即f(-x)=-f(x)对任意x∈R成立，所以f(x)是奇函数．---------------------------------------3分

    （2）设则

    所以f(x)是增函数．----------------------------------------------------6分

    (3)解：∵由（2）知f(x) 在R上是单调增函数，又由(1)f(x)是奇函数．

    f(k?3)＜-f(3-9-2)=f(-3+9+2)，  k?3＜-3+9+2，

    3-(1+k)?3+2＞0对任意x∈R成立．

    令t=3＞0，问题等价于t-(1+k)t+2＞0对任意t＞0恒成立．

    R恒成立．

    ---------------------------------------------------------------------------12分

     

     


    同步练习册答案