
题目列表(包括答案和解析)
(本题满分14分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,且过点
的图象上,且过点![]() 的切线的斜率为
的切线的斜率为![]() .
.
(1)求数列![]() 的通项公式;(2)若
的通项公式;(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,![]() ,求
,求![]() 的通项公式.
的通项公式.
(本题满分14分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() N*),其中
N*),其中![]() .
.
(Ⅰ) 求![]() 的通项公式;
的通项公式;
(Ⅱ) 设![]() (
(![]() N*).
N*).
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
①证明: ![]() ;
;
② 求证:![]() .
.
(本题满分14分)
已知数列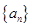 的前
的前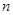 项和为
项和为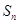 ,且
,且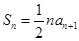 (
(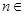 N*),其中
N*),其中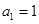 .
.
(Ⅰ)求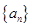 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明: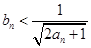 ;
;
② 求证: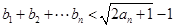 .
.
(本题满分14分)已知数列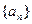 的前
的前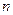 项和
项和 ,数列
,数列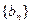 为等比数列,且满足
为等比数列,且满足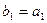 ,
,
(1)求数列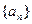 ,
,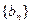 的通项公式;
的通项公式;
(2)求数列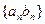 的前
的前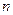 项和。
项和。
(本题满分14分)已知数列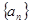 的前
的前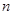 项和为
项和为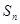 ,
,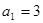 ,若数列
,若数列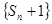 是公比为
是公比为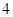 的等比数列.
的等比数列.
(Ⅰ)求数列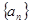 的通项公式
的通项公式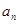 ;
;
(Ⅱ)设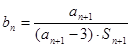 ,
,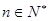 ,求数列
,求数列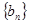 的前
的前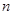 项和
项和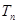 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com