
题目列表(包括答案和解析)
如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
, ![]() 为线段
为线段![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的余弦值.
的余弦值.

(本题满分12分)
如图1,在直角梯形 中,
中, ,
, ,
, ,
,  为线段
为线段 的中点.将
的中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.

(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求二面角 的余弦值.
的余弦值.

如图,在直角梯形 中,
中, ,
,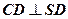 ,
,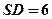 ,
, ,
,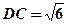 ,
, 是
是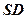 的中点,
的中点,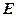 是线段
是线段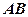 的中点,沿
的中点,沿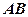 把平面
把平面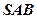 折起到平面
折起到平面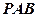 的位置,使
的位置,使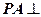 平面
平面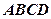 ,则下列命题正确的个数是 。
,则下列命题正确的个数是 。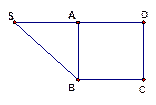
(1)二面角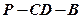 成角
成角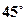 ;
;
(2)设折起后几何体的棱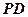 的中点
的中点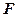 ,则
,则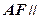 平面
平面 ;
;
(3)平面 和平面
和平面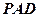 所成的锐二面角的大小为
所成的锐二面角的大小为 ;
;
(4)点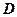 到平面
到平面 的距离为
的距离为
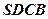 中,
中,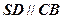 ,
,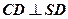 ,
,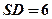 ,
,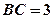 ,
,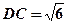 ,
,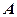 是
是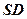 的中点,
的中点,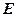 是线段
是线段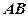 的中点,沿
的中点,沿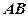 把平面
把平面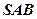 折起到平面
折起到平面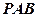 的位置,使
的位置,使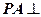 平面
平面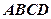 ,则下列命题正确的个数是 。
,则下列命题正确的个数是 。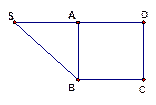
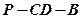 成角
成角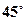 ;
;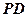 的中点
的中点 ,则
,则 平面
平面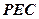 ;
;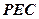 和平面
和平面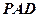 所成的锐二面角的大小为
所成的锐二面角的大小为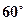 ;
;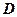 到平面
到平面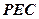 的距离为
的距离为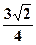
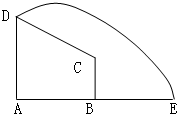 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=| 3 |
一、选择题:
题号
1
2
3
4
5
6
7
8
选项
C
A
C
D
C
A
A
D
二、填空题(每题5分,共30分,两空的前一空3分,后一空2分)
9. 10.
10. 11.
11. 12.
12. 13.
13.
14.1或7, 15.
15. 
三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.
16.(本题满分12分)
解:(Ⅰ)由图象知
 的最小正周期
的最小正周期 ,故
,故 ……3分
……3分
将点 代入
代入 的解析式得
的解析式得 ,又
,又 ,
,
∴
故函数 的解析式为
的解析式为 ……6分
……6分

 (Ⅱ)变换过程如下:
(Ⅱ)变换过程如下:
|