
题目列表(包括答案和解析)
 ,a1=2
,a1=2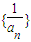 的前n项和Tn;
的前n项和Tn;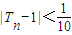 成立.若存在,请找出一个这样的集合;若不存在,请说明理由.
成立.若存在,请找出一个这样的集合;若不存在,请说明理由.
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
 (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为
锐角三角形时t的取值范围.
已知数列![]()
![]() 的前
的前![]()
![]() 项和为
项和为![]()
![]() ,通项为
,通项为![]()
![]() ,且满足
,且满足![]()
![]() (
(![]()
![]() 是常数且
是常数且![]()
![]() ).
).
(I)求数列![]()
![]() 的通项公式;
的通项公式;
(II) 当![]()
![]() 时,试证明
时,试证明![]()
![]() ;
;
(III)设函数![]()
![]() ,
,![]()
![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使
,使![]()
![]() 对
对![]()
![]() 都成立?若存在,求出
都成立?若存在,求出![]()
![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
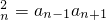 ,n∈N*.
,n∈N*.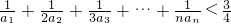 .
.| an |
| an-1 |
| n+1 |
| n-1 |
| 1 |
| an |
| 1 |
| 10 |
一、选择题:
题号
1
2
3
4
5
6
7
8
选项
C
A
C
D
C
A
A
D
二、填空题(每题5分,共30分,两空的前一空3分,后一空2分)
9. 10.
10. 11.
11. 12.
12. 13.
13.
14.1或7, 15.
15. 
三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.
16.(本题满分12分)
解:(Ⅰ)由图象知
 的最小正周期
的最小正周期 ,故
,故 ……3分
……3分
将点 代入
代入 的解析式得
的解析式得 ,又
,又 ,
,
∴
故函数 的解析式为
的解析式为 ……6分
……6分

 (Ⅱ)变换过程如下:
(Ⅱ)变换过程如下:
|