
题目列表(包括答案和解析)
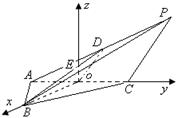
如图,在三棱锥![]() 中,
中,![]() 是正三角形,
是正三角形,![]() ,D是
,D是![]() 的中点,二面角
的中点,二面角![]() 为120,
为120,![]() ,
,![]() .取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
.取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
(I)求B、D、P三点的坐标;
(II)求异面直线AB与PC所成的角;
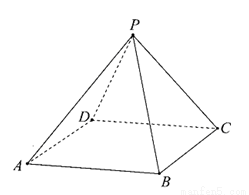
如图,在底面是正方形的四棱锥P—ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
(I)求证:PD⊥BC;
(II)求二面角B—PD—C的正切值。
【解析】第一问利用∵平面PCD⊥平面ABCD,又∵平面PCD∩平面ABCD=CD,
BC在平面ABCD内 ,BC⊥CD,∴BC⊥平面PCD.
∴PD⊥BC.
第二问中解:取PD的中点E,连接CE、BE,
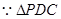 为正三角形,
为正三角形,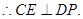
由(I)知BC⊥平面PCD,∴CE是BE在平面PCD内的射影,
∴BE⊥PD.∴∠CEB为二面角B—PD—C的平面角,进而求解。
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(12分)
学校欲在操场边上一直角三角形空地ABC上种植草坪,并需铺设一根水管EF(E在AC上,F在AB上)用于灌溉,已知∠A=30°,∠C=90°,BC=2a,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF=60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。

(1)比较甲乙两种方案,哪一种方案更合理(EF的长较小的合理);
(2)学校研究小组通过研究得出:无论D在BC的什么位置,总存在E,F两点,使△DEF为正三角形。试证明该结论的正确性。
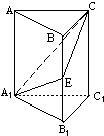
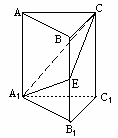
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
(Ⅰ)求证:BE=EB1;
(Ⅱ)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
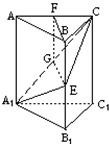
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).

(Ⅰ)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
① ∵
∴EG⊥侧面AC1;取AC的中点F,连结BF,FG,由AB=BC得BF⊥AC,
② ∵
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③ ∵
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④ ∵
∴FG∥AA1,△AA1C∽△FGC,
⑤ ∵
![]() 即
即![]() ,故
,故![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com