
题目列表(包括答案和解析)

![]() 内的概率为
内的概率为![]() .
.
(i)当点C在圆周上运动时,求![]() 的最大值;
的最大值;
(ii)记平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
![]() ,当
,当![]() 取最大值时,
取最大值时,
求![]() 的值。
的值。
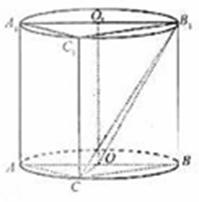
题干

概率为![]() 。
。
(i)当点C在圆周上运动时,求![]() 的最大值;
的最大值;
(ii)记平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
![]() ,当
,当![]() 取最大值时,求
取最大值时,求![]() 的值。
的值。
题干

概率为![]() 。
。
(i)当点C在圆周上运动时,求![]() 的最大值;
的最大值;
(ii)记平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
![]() ,当
,当![]() 取最大值时,求
取最大值时,求![]() 的值。
的值。
| 1 | 2 |
 .
.
一、选择题:本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个是符合题目要求的。
1―8 BDCAABCB
二、填空题:本大题共有6个小题,每小题5分,共30分;请把答案写在相应的位置上。
9..files/image133.gif) 10.
10..files/image135.gif) 11.7 12.
11.7 12..files/image137.gif) 13.
13..files/image139.gif) 14.
14..files/image141.gif)
三、解答题:本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤。
15.(本题满分13分)
解:.files/image143.gif)
(1).files/image145.gif)
.files/image147.gif)
(2)由(1)知,.files/image149.gif)
.files/image151.gif)
16.(本题满分13分)
解:(1).files/image109.gif) 表示经过操作以后
表示经过操作以后.files/image154.gif) 袋中只有1个红球,有两种情形出现
袋中只有1个红球,有两种情形出现
①先从.files/image154.gif) 中取出
中取出.files/image156.gif) 红和
红和.files/image156.gif) 白,再从
白,再从.files/image159.gif) 中取一白到
中取一白到.files/image154.gif) 中
中
.files/image161.gif)
②先从.files/image154.gif) 中取出
中取出.files/image163.gif) 红球,再从
红球,再从.files/image159.gif) 中取一红球到
中取一红球到.files/image154.gif) 中
中
.files/image165.gif)
∴.files/image167.gif) 。 ………………7分
。 ………………7分
(2)同(1)中计算方法可知:.files/image169.gif) 。
。
于是.files/image111.gif) 的概率分布列
的概率分布列
.files/image111.gif)
0
1
2
3
P
.files/image172.gif)
.files/image174.gif)
.files/image174.gif)
.files/image172.gif)
.files/image176.gif) 。 ………………13分
。 ………………13分
17.(本题满分13分)
解法1:(1)连结MA、B
|