
题目列表(包括答案和解析)
.若直线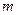 被两平行线
被两平行线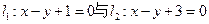 所截得的线段的长为
所截得的线段的长为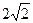 ,则
,则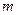 的倾斜
的倾斜 角可以是
角可以是
①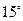 ②
②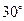 ③
③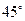 ④
④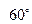 ⑤
⑤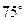
其中正确答案的序号是 .(写出所有正确答案的序号)
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(选修4—2 矩阵与变换)(本小题满分7分)
已知矩阵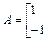
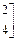 ,向量
,向量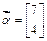 .
.
(Ⅰ) 求矩阵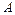 的特征值
的特征值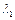 、
、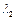 和特征向量
和特征向量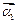 、
、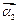 ;
;
(Ⅱ)求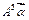 的值.
的值.
(2)(选修4—4 参数方程与极坐标)(本小题满分7分)
在极坐标系中,过曲线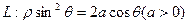 外的一点
外的一点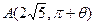 (其中
(其中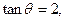
 为锐角)作平行于
为锐角)作平行于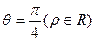 的直线
的直线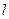 与曲线分别交于
与曲线分别交于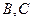 .
.
(Ⅰ) 写出曲线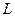 和直线
和直线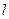 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为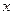 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若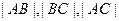 成等比数列,求
成等比数列,求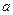 的值.
的值.
(3)(选修4—5 不等式证明选讲)(本小题满分7分)
已知正实数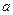 、
、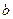 、
、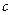 满足条件
满足条件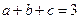 ,
,
(Ⅰ) 求证: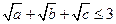 ;
;
(Ⅱ)若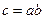 ,求
,求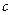 的最大值.
的最大值.
.15. (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
A.(不等式选做题)不等式 的解集为 .
的解集为 .
B.(几何证明选做题)如图,直线 与圆
与圆 相切于点
相切于点 ,割线
,割线 经过圆心
经过圆心 ,弦
,弦 ⊥
⊥ 于点
于点 ,
,  ,
, ,则
,则 .
.
C.(坐标系与参数方程选做题)在极坐标系中,圆 的圆心到直线
的圆心到直线 的距离为 .
的距离为 .
.(本小题满分12分)
某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
| 休假次数 |  | 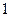 | 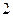 | 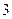 |
| 人数 | 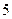 | 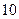 | 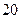 | 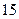 |
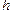 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数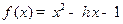 在区间
在区间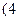 ,
,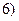 上有且只有一个零点”为事件
上有且只有一个零点”为事件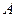 ,求事件
,求事件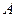 发生的概率
发生的概率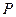 ;
;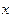 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量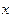 的分布列及数学期望
的分布列及数学期望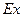 .
.1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B 
11.A 12.D
【解析】
1. ,所以选B.
,所以选B.
2. 的系数是
的系数是 ,所以选B.
,所以选B.
3. ,所以选
,所以选 .
.
4. 为钝角或
为钝角或 ,所以选C
,所以选C
5. ,所以选C.
,所以选C.
6. ,所以选B.
,所以选B.
7. ,所以选D.
,所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9.将 左移
左移 个单位得
个单位得 ,所以选A.
,所以选A.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.画可行域 可知符合条件的点 是:
是: 共6个点,故
共6个点,故 ,所以选D.
,所以选D.
二、
13.185. .
.
14.60. .
.
15. ,由
,由 ,得
,得
 .
.
16. .如图:
.如图:

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)由三角函数的定义知: .
.
(2)


 .
.
18.(1)设两年后出口额恰好达到危机前出口额的事件为 ,则
,则 .
.
(2)设两年后出口额超过危机前出口额的事件为 ,则
,则 .
.
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)


(2)

又


综上: .
.
21.(1) 的解集为(1,3)
的解集为(1,3)
∴1和3是 的两根且
的两根且
|