
题目列表(包括答案和解析)
设关于x的函数![]() 的最小值为
的最小值为![]() .
.
⑴写出![]() 的表达式;w.w.w.k.s.5.u.c.o.m
的表达式;w.w.w.k.s.5.u.c.o.m ![]()
![]()
⑵试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() 的最大值.
的最大值.
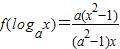 ,
,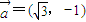 ,
,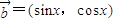 ,函数
,函数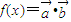
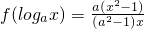 ,
,已知函数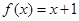 ,设
,设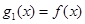 ,
,
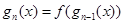
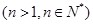 .
.
(1)猜测并直接写出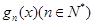 的表达式;此时若设
的表达式;此时若设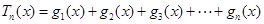 ,且关于
,且关于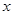 的函数
的函数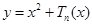
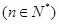 在区间
在区间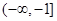 上的最小值为
上的最小值为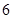 ,则求
,则求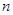 的值;
的值;
(2)设数列 为等比数列,数列
为等比数列,数列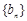 满足
满足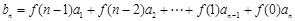 ,
,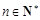 ,若
,若
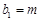 ,
,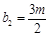 ,其中
,其中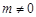 ,则
,则
①当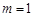 时,求
时,求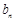 ;
;
②设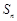 为数列
为数列 的前
的前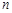 项和,若对于任意的正整数
项和,若对于任意的正整数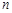 ,都有
,都有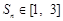 ,求实数
,求实数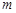 的取值范围.
的取值范围.
1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B 
11.A 12.D
【解析】
1. ,所以选B.
,所以选B.
2. 的系数是
的系数是 ,所以选B.
,所以选B.
3. ,所以选
,所以选 .
.
4. 为钝角或
为钝角或 ,所以选C
,所以选C
5. ,所以选C.
,所以选C.
6. ,所以选B.
,所以选B.
7. ,所以选D.
,所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9.将 左移
左移 个单位得
个单位得 ,所以选A.
,所以选A.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.画可行域 可知符合条件的点 是:
是: 共6个点,故
共6个点,故 ,所以选D.
,所以选D.
二、
13.185. .
.
14.60. .
.
15. ,由
,由 ,得
,得
 .
.
16. .如图:
.如图:

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)由三角函数的定义知: .
.
(2)


 .
.
18.(1)设两年后出口额恰好达到危机前出口额的事件为 ,则
,则 .
.
(2)设两年后出口额超过危机前出口额的事件为 ,则
,则 .
.
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)


(2)

又


综上: .
.
21.(1) 的解集为(1,3)
的解集为(1,3)
∴1和3是 的两根且
的两根且
|