
题目列表(包括答案和解析)
设抛物线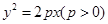 的焦点为
的焦点为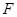 ,点
,点 ,线段
,线段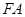 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线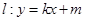 与抛物线相切于点
与抛物线相切于点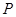 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点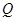 ,以
,以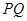 为直径的圆记为圆
为直径的圆记为圆 .
.
(1)求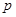 的值;
的值;
(2)证明:圆 与
与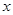 轴必有公共点;
轴必有公共点;
(3)在坐标平面上是否存在定点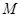 ,使得圆
,使得圆 恒过点
恒过点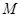 ?若存在,求出
?若存在,求出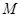 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知点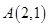 在抛物线
在抛物线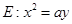 上,直线
上,直线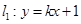 (
( ,且
,且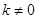 )与抛物线
)与抛物线 ,相交于
,相交于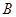 、
、 两点,直线
两点,直线 、
、 分别交直线
分别交直线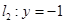 于点
于点 、
、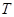 .
.
(1)求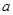 的值;
的值;
(2)若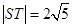 ,求直线
,求直线 的方程;
的方程;
(3)试判断以线段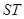 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
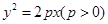 的焦点为
的焦点为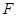 ,点
,点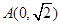 ,线段
,线段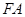 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线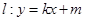 与抛物线相切于点
与抛物线相切于点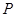 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点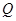 ,以
,以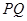 为直径的圆记为圆
为直径的圆记为圆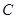 .
.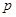 的值;
的值;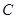 与
与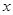 轴必有公共点;
轴必有公共点;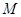 ,使得圆
,使得圆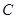 恒过点
恒过点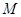 ?若存在,求出
?若存在,求出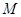 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.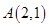 在抛物线
在抛物线 上,直线
上,直线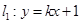 (
(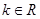 ,且
,且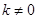 )与抛物线
)与抛物线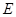 ,相交于
,相交于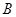 、
、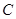 两点,直线
两点,直线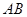 、
、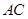 分别交直线
分别交直线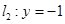 于点
于点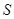 、
、 .
.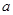 的值;
的值;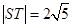 ,求直线
,求直线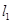 的方程;
的方程; 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
1.B 2.C 3.B 4.C 5.B 6.B 7.C 8.B 9.C 10.B 
11.C 12.D
【解析】
3.当 时,函数
时,函数 在
在 上,
上, 恒成立即
恒成立即 在
在 上恒成立,可得
上恒成立,可得

当 时,函数
时,函数 在
在 上,
上, 恒成立
恒成立
即 在
在 上恒成立
上恒成立
可得 ,对于任意
,对于任意 恒成立
恒成立
所以 ,综上得
,综上得 .
.
4.解法一:联立 ,得
,得 .
.
 方程总有解,需
方程总有解,需 恒成立
恒成立
即 恒成立,得
恒成立,得 恒成立
恒成立
 ;又
;又

 的取值范围为
的取值范围为 .
.
解法二:数形结合,因为直线 恒过定点(0,1),要使直线与椭圆
恒过定点(0,1),要使直线与椭圆 总有交点当日仅当点(0,1)在椭圆上或椭圆内,即
总有交点当日仅当点(0,1)在椭圆上或椭圆内,即

 又
又

 的取值范围为
的取值范围为 .
.
5.

7.展开式前三项的系数满足 可解得
可解得 ,或
,或 (舍去).从而可知有理项为
(舍去).从而可知有理项为 ,故C正确.
,故C正确.
8. ,欲使
,欲使 为奇函数,须使
为奇函数,须使 ,观察可知,
,观察可知, 、
、 不符合要求,若
不符合要求,若 ,则
,则
 ,其在
,其在 上是减函数,故B正确
上是减函数,故B正确
当 时,
时, ,其在
,其在 上是增函数,不符合要求.
上是增函数,不符合要求.
9. 等价于
等价于

画图可知 ,故
,故 .
.
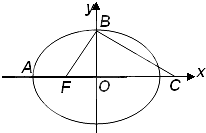
10.如图乙所示.设 ,点
,点 到直线
到直线 的距离为
的距离为 ,则由抛物线定义得
,则由抛物线定义得 ,
,

又由点 在椭圆上,及椭圆第一定义得
在椭圆上,及椭圆第一定义得
由椭圆第二定义得 ,解之得
,解之得 .
.
11.从52张牌中任意取13张牌的全部取法为 ;缺少某一种花色的取法为
;缺少某一种花色的取法为 ,缺少两种花色的取法为
,缺少两种花色的取法为 ,缺少三种花色的取法为
,缺少三种花色的取法为 ,根据容斥原理可知四种花色齐全的取法为
,根据容斥原理可知四种花色齐全的取法为 .
.
12.设 中点为
中点为 ,连
,连 .由已知得
.由已知得 平面
平面 ,作
,作 ,交
,交 的延长线于点
的延长线于点 ,连
,连 .则
.则 为所求,设
为所求,设 ,则
,则 ,在
,在
中可求出 ,则
,则 .
.
二、填空题
13. .
.
提示:可以用换元法,原不等式为 也可以用数形结合法.
也可以用数形结合法.
令 ,在同一坐标系内分别画出这两个函数的图象,由图直观得解集.
,在同一坐标系内分别画出这两个函数的图象,由图直观得解集.
14.12 .提示:经判断,
.提示:经判断, 为截面团的直径,再由巳知可求出球的半径为
为截面团的直径,再由巳知可求出球的半径为 .
.
15. .提示:由于
.提示:由于 得
得
解得 ,又
,又

所以,当 时,
时, 取得最小值.
取得最小值.
16.①②④
三、解答题
17.懈:
 ,由正弦定理得,
,由正弦定理得,

 又
又 ,
,
 ,化简得
,化简得
 为等边三角形.
为等边三角形.
说明;本题是向量和三角相结合的题目,既考查了向量的基本知识,又考查了三角的有关知识,三角形的形状既可由角确定。也可由边确定,因此既可从角入手,把边化为角;也可从边入手,把角化为边来判断三角形的形状.
18.解:(1)在第一次更换灯泡工作中,不需要更换灯泡的概率为 需要更换2只灯泡的概率为
需要更换2只灯泡的概率为 .
.
(2)对该盏灯来说,在第1、2次都更换了灯泡的概率为 ,在第一次未更换灯泡而在第二次需要更换灯泡的概率为
,在第一次未更换灯泡而在第二次需要更换灯泡的概率为 ,故所求的概率为
,故所求的概率为 .
.
(3)当 时,
时,
由(2)知第二次灯泡更换工作中,某盏灯更换的概率
故至少换4只灯泡的概率为



19.解: ]
]
因为函数 在
在 处的切线斜率为
处的切线斜率为
所以
即 ①
①
又
得 ②
②
(1)函数 在
在 时有极值
时有极值
 ③
③
解式①②③得
所以 .
.
(2)因为函数 在区间
在区间 上单调递增,所以导函数
上单调递增,所以导函数 在区间
在区间 的值恒大于或等于零.
的值恒大于或等于零.
则
得 ,所以实数
,所以实数 的取值范围为
的取值范围为 .
.
20.解:(1)连接 因为
因为 平面
平面 ,平面
,平面 平面
平面
所以 ;又
;又 为
为 的中点,故
的中点,故 为
为 的中点
的中点

 底面
底面
 为
为 与底面
与底面 所成的角
所成的角
在 中,
中,

 所以
所以 与底面
与底面 所成的角为45°.
所成的角为45°.
(2)解法一;如图建立直角坐标系
则 ,
, 
 设
设 点的坐标为
点的坐标为
故



 点
点 的坐标为
的坐标为

故 .
.
解法二: 平面
平面
 ,又
,又
 平面
平面
在正方形 中,
中,
 .
.
21.解:(1)设点 、
、 的坐标分别为
的坐标分别为 、
、 ,点
,点 的坐标为
的坐标为
当 时,设直线
时,设直线 的斜率为
的斜率为
 直线
直线 过点
过点
 的方程为
的方程为
又已知 ①
①
 ②
②
 ③
③
 ④
④
∴式①一式②得
 ⑤
⑤
③式+式④得
 ⑥
⑥
∴由式⑤、式⑥及
得点 的坐标满足方程
的坐标满足方程
 ⑦
⑦
当 时,
时, 不存在,此时
不存在,此时 平行于
平行于 轴,因此
轴,因此 的中点
的中点 一定落在
一定落在 轴上,即
轴上,即 的坐标为
的坐标为 ,显然点
,显然点 (
( ,0)满足方程⑦
,0)满足方程⑦
综上,点 的坐标满足方程
的坐标满足方程
设方程⑦所表示的曲线为
则由 ,
,
得
因为 ,又已知
,又已知 ,
,
所以当 时.
时. ,曲线
,曲线 与椭圆
与椭圆 有且只有一个交点
有且只有一个交点 ,
,
当 时,
时, ,曲线
,曲线 与椭圆
与椭圆 没有交点,因为(0,0)在椭圆内,又在曲线
没有交点,因为(0,0)在椭圆内,又在曲线 上,所以曲线
上,所以曲线 在椭圆内,故点
在椭圆内,故点 的轨迹方程为
的轨迹方程为

(2)由 解得曲线
解得曲线 与
与 轴交于点(0,0),(0,
轴交于点(0,0),(0, )
)
由 解得曲线
解得曲线 与
与 轴交于点(0,0).(
轴交于点(0,0).( ,0)
,0)
当 ,即点
,即点 为原点时,(
为原点时,( ,0)、(0,
,0)、(0, )与(0.0)重合,曲线
)与(0.0)重合,曲线 与坐标轴只有一个交点(0,0).
与坐标轴只有一个交点(0,0).
当 ,且
,且 ,即点
,即点 不在椭圆
不在椭圆 外且在除去原点的
外且在除去原点的 轴上时,曲线
轴上时,曲线 与坐标轴有两个交点(0,
与坐标轴有两个交点(0, )与(0,0),同理,当
)与(0,0),同理,当 且
且 时,曲线与坐标轴有两个交点(
时,曲线与坐标轴有两个交点( ,o)、(0,0).
,o)、(0,0).
当 ,且
,且 时,即点
时,即点 不在椭圆
不在椭圆 且不在坐标轴上时,曲线与坐标轴有三个交点(
且不在坐标轴上时,曲线与坐标轴有三个交点( ,0)、(0,
,0)、(0, )与(0,0).
)与(0,0).
22.(1)解: ,又
,又
 是以首项为
是以首项为 ,公比为
,公比为 的等比数列.
的等比数列.
 .
.
(2)证明:设数列 的公比为
的公比为 ,则条件等式可化为:
,则条件等式可化为:
 数列
数列 为等差数列,
为等差数列,
(3)证明:由题意知
 ①
①
式① 得
得
 ②
②
式①-式②得



 .
.
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com