题目列表(包括答案和解析)
以原点O及点A（5，2）为顶点作等腰直角三角形OAB，使
，则
的坐标为（ ）。
A、（2，-5） B、（-2，5）或（2，-5）
C、（-2，5） D、（7，-3）或（3，7）
以O为原点，
所在直线为
轴，建立如 所示的坐标系。设
，点F的坐标为
，
，点G的坐标为
。
（1）求
关于
的函数
的表达式，判断函数
的单调性，并证明你的判断；
（2）设ΔOFG的面积
，若以O为中心，F为焦点的椭圆经过点G，求当
取最小值时椭圆的方程；
（3）在（2）的条件下，若点P的坐标为
，C、D是椭圆上的两点，且
，求实数
的取值范围。
从原点出发的某质点M，按向量a=(0,1)移动的概率为
，按向量b=（0，2）移动的概率为
，设M可到达点（0，n）的概率为Pn
(1)求P1和P2的值；（2）求证：
=
;(3)求
的表达式。
为了得到函数
的图象，只要把函数
的图象上所有点的
A. 横坐标缩短到原来的
倍（纵坐标不变），再把所得图象上所有的点向左平移
个单位长度。
B. 横坐标伸长到原来的2倍（纵坐标不变），再把所得图象上所有点的向左平移个单位长度。
C. 向右平移
个单位长度，再把所得图象上所有的点横坐标缩短到原来的倍（纵坐标不变）
D. 向左平移个单位长度，再把所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）
（本小题满分12分）已知函数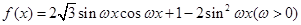
，
且函数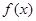
的最小正周期为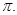
（1）若
，求函数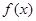的单调递减区间；
（2）将函数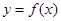
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
，把所得到的图象再向左平移
个单位，得到函数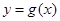
的图象，求函数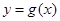在区间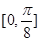
上的最小值。
一、选择题（4′×10=40分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空题（4′×4=16分）
11．
12．
13．
14．
三、解答题（共44分）
15．①解：原不等式可化为：
………………………2′
作根轴图：
………………………4′
可得原不等式的解集为：
………………………6′
②解：直线
的斜率
………………………2′
∵直线
与该直线垂直
∴
则的方程为：
………………………4′
即
为所求………………………6′
16．解：∵
则
，
且
………………………1′
∴有
………………………3′
………………………4′
………………………5′
当且仅当：
即
………………………5′
亦:
时取等号
所以:当
时,
………………………7′
17．解：将
代入
中变形整理得：
………………………2′
首先
且
………………………3′
设
由题意得：
解得：
或
（舍去）………………………6′
由弦长公式得：
………………………8′
18．解①设双曲线的实半轴，虚半轴分别为
，
则有：
∴
………………………1′
于是可设双曲线方程为：
①或
②………………………3′
将点
代入①求得：
将点代入②求得：
(舍去) ………………………4′
∴, 
∴双曲线的方程为：
………………………5′
②由①解得:
,
,
,焦点在
轴上………………………6′
∴双曲线的准线方程为:
………………………7′
渐近线方程为: 
………………………8′
19．解：①设
为椭圆的半焦距,则
,
∵
∴
∴
………………………1′
将
代入
,可求得
∵
∴
即
又
、
………………………3′
∴
，
∵
………………………5′
∴
从而
∴离心率
………………………6′
②由抛物线的通径
得抛物线方程为
，其焦点为
………………………7′
∴椭圆的左焦点
∴
由①解得：
∴
………………………8′
∴该椭圆方程为：
………………………9′
③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com