题目列表(包括答案和解析)
| x |
| 16 |
| y |
| 12 |
| 3 |
在平面直角坐标系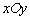
中，若中心在坐标原点上的双曲线的一条准线方程为
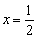，且它的一个顶点与抛物线
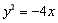的焦点重合，则该双曲线的渐进线方程为 .
设椭圆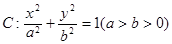
的一个顶点与抛物线
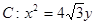的焦点重合，
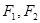分别是椭圆的左、右焦点，且离心率
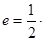且过椭圆右焦点
的直线
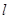与椭圆C交于
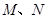两点.
（1）求椭圆C的方程；
（2）是否存在直线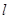，使得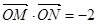
.若存在，求出直线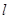的方程；若不存在，说明理由.
（3）若AB是椭圆C经过原点O的弦，
MN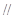
AB，求证：
为定值
在平面直角坐标系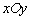
中，若中心在坐标原点上的双曲线的一条准线方程为
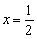，且它的一个顶点与抛物线
的焦点重合，则该双曲线的渐进线方程为 .
一、选择题（4′×10=40分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空题（4′×4=16分）
11．
12．
13．
14．
三、解答题（共44分）
15．①解：原不等式可化为：
………………………2′
作根轴图：
………………………4′
可得原不等式的解集为：
………………………6′
②解：直线
的斜率
………………………2′
∵直线
与该直线垂直
∴
则的方程为：
………………………4′
即
为所求………………………6′
16．解：∵
则
，
且
………………………1′
∴有
………………………3′
………………………4′
………………………5′
当且仅当：
即
………………………5′
亦:
时取等号
所以:当
时,
………………………7′
17．解：将
代入
中变形整理得：
………………………2′
首先
且
………………………3′
设
由题意得：
解得：
或
（舍去）………………………6′
由弦长公式得：
………………………8′
18．解①设双曲线的实半轴，虚半轴分别为
，
则有：
∴
………………………1′
于是可设双曲线方程为：
①或
②………………………3′
将点
代入①求得：
将点代入②求得：
(舍去) ………………………4′
∴, 
∴双曲线的方程为：
………………………5′
②由①解得:
,
,
,焦点在
轴上………………………6′
∴双曲线的准线方程为:
………………………7′
渐近线方程为: 
………………………8′
19．解：①设
为椭圆的半焦距,则
,
∵
∴
∴
………………………1′
将
代入
,可求得
∵
∴
即
又
、
………………………3′
∴
，
∵
………………………5′
∴
从而
∴离心率
………………………6′
②由抛物线的通径
得抛物线方程为
，其焦点为
………………………7′
∴椭圆的左焦点
∴
由①解得：
∴
………………………8′
∴该椭圆方程为：
………………………9′
③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com