
题目列表(包括答案和解析)
设数列 的前
的前 项和为
项和为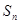 ,对任意的正整数
,对任意的正整数 ,都有
,都有 成立,记
成立,记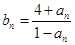 .(1)(1)求数列
.(1)(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为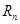 ,是否存在正整数
,是否存在正整数 ,使得
,使得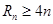 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记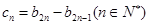 ,设数列
,设数列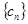 的前
的前 项和为
项和为 ,求证:对于
,求证:对于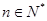 都有
都有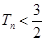
 的前
的前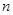 项和为
项和为 ,对任意的正整数
,对任意的正整数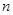 ,都有
,都有 成立,记
成立,记 .(1)(1)求数列
.(1)(1)求数列 与数列
与数列 的通项公式;
的通项公式; 的前
的前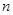 项和为
项和为 ,是否存在正整数
,是否存在正整数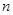 ,使得
,使得 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数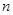 ;若不存在,请说明理由.
;若不存在,请说明理由. ,设数列
,设数列 的前
的前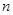 项和为
项和为 ,求证:对于
,求证:对于 都有
都有
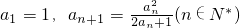
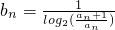 ,若对于任意正整数n都有
,若对于任意正整数n都有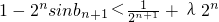 成立,求实数λ的取值范围.
成立,求实数λ的取值范围.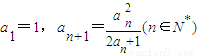
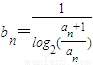 ,若对于任意正整数n都有
,若对于任意正整数n都有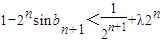 成立,求实数λ的取值范围.
成立,求实数λ的取值范围.| 1 |
| f(n) |
| 1 |
| 2n |
| 4 |
| 35 |
| 1 |
| 2 |
| 1 |
| 2 |
一、选择题(每小题5分,满分60分)
1
2
3
4
5
6
7
8
9
10
11
12
B
B
C
D
A
C
A
B
A
C
A
D
二、填空题(每小题4分,满分16分)
13.卷.files/image290.gif) 14.
14.卷.files/image292.gif) 15.100
16.③④
15.100
16.③④
三、解答题(第17、18、19、20、21题各12分,第22题14分,共74分)
17.(I)卷.files/image294.gif)
卷.files/image296.gif)
(Ⅱ)卷.files/image298.gif)
卷.files/image300.gif)
卷.files/image302.gif)
卷.files/image303.jpg)
卷.files/image305.gif)
卷.files/image307.gif) 函数
函数卷.files/image248.gif) 的值域为
的值域为卷.files/image310.gif)
18.解:(I)记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件
卷.files/image002.gif) 、
、卷.files/image004.gif) 、
、卷.files/image314.gif) ,则
,则卷.files/image316.gif) ,且有
,且有卷.files/image318.gif) 即
即卷.files/image320.gif)
卷.files/image322.gif)
(Ⅱ)卷.files/image226.gif) 的可能取值:0,1,2,3
的可能取值:0,1,2,3
卷.files/image325.gif)
卷.files/image226.gif)
0
1
2
3
卷.files/image328.gif)
卷.files/image330.gif)
卷.files/image332.gif)
卷.files/image334.gif)
卷.files/image336.gif)
卷.files/image338.gif)
19.(I)设卷.files/image340.gif) 是
是卷.files/image342.gif) 的中点,连结
的中点,连结卷.files/image344.gif) ,
,
则四边形卷.files/image346.gif) 为方形,
为方形,卷.files/image348.gif) ,故
,故卷.files/image350.gif) ,
,
卷.files/image352.gif) 即
即卷.files/image354.gif)
又卷.files/image356.gif)
卷.files/image358.gif) 平面
平面卷.files/image360.gif)
(Ⅱ)由(I)知卷.files/image240.gif) 平面
平面卷.files/image360.gif) ,
,
又卷.files/image364.gif) 平面
平面卷.files/image360.gif) ,
,卷.files/image367.gif) ,
,
取卷.files/image369.gif) 的中点
的中点卷.files/image263.gif) ,连结
,连结卷.files/image372.gif) 又
又卷.files/image374.gif) ,
,
卷.files/image229.jpg) 则
则卷.files/image376.gif) ,取
,取卷.files/image378.gif) 的中点
的中点卷.files/image153.gif) ,连结
,连结卷.files/image381.gif) 则
则卷.files/image383.gif)
卷.files/image385.gif) 为二面角
为二面角卷.files/image244.gif) 的平面角
的平面角
连结卷.files/image388.gif) ,在
,在卷.files/image390.gif) 中,
中,卷.files/image392.gif) ,
,
取卷.files/image394.gif) 的中点
的中点卷.files/image396.gif) ,连结
,连结卷.files/image398.gif) ,
,卷.files/image400.gif) ,在
,在卷.files/image402.gif) 中,
中,
卷.files/image404.gif)
卷.files/image307.gif) 二面角
二面角卷.files/image244.gif) 的余弦值为
的余弦值为卷.files/image408.gif)
法二:
(I)以卷.files/image410.gif) 为原点,
为原点,卷.files/image412.gif) 所在直线分别为
所在直线分别为卷.files/image098.gif) 轴,
轴,卷.files/image415.gif) 轴,
轴,卷.files/image417.gif) 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则卷.files/image419.gif)
卷.files/image421.gif)
卷.files/image423.gif)
又因为卷.files/image425.gif)
所以,卷.files/image240.gif) 平面
平面卷.files/image242.gif)
(Ⅱ)设卷.files/image429.gif) 为平面
为平面卷.files/image431.gif) 的一个法向量。
的一个法向量。
由卷.files/image433.gif) 得
得卷.files/image435.gif)
取卷.files/image437.gif) ,则
,则卷.files/image439.gif) 又
又卷.files/image441.gif) ,
,
设卷.files/image443.gif) 为平面
为平面卷.files/image445.gif) 的一个法向量,由
的一个法向量,由卷.files/image447.gif) ,
,卷.files/image449.gif) ,
,
得卷.files/image451.gif) 取
取卷.files/image453.gif) 取
取卷.files/image455.gif)
设卷.files/image457.gif) 与
与卷.files/image021.gif) 的夹角为
的夹角为卷.files/image460.gif) ,二面角
,二面角卷.files/image244.gif) 为
为卷.files/image463.gif) ,显然
,显然卷.files/image463.gif) 为锐角,
为锐角,
卷.files/image466.gif) ,即为所求
,即为所求
20.解:(I)定义域为卷.files/image468.gif)
卷.files/image470.gif) 时,
时,卷.files/image472.gif) 时,
时,卷.files/image474.gif)
故卷.files/image476.gif) 的单调递增区间是
的单调递增区间是卷.files/image478.gif) ,单调递减区间是
,单调递减区间是卷.files/image480.gif)
(Ⅱ)卷.files/image482.gif) 即:
即:卷.files/image484.gif) 令
令卷.files/image486.gif)
卷.files/image488.gif)
卷.files/image489.jpg) 所以
所以卷.files/image491.gif)
卷.files/image493.gif) 在
在卷.files/image495.gif) 单调递减,在
单调递减,在卷.files/image497.gif) 上单调递增
上单调递增
卷.files/image251.gif) 在
在卷.files/image500.gif) 上有两个相异实根
上有两个相异实根
卷.files/image502.gif)
21.解:(I)由题意知:卷.files/image504.gif)
卷.files/image506.gif)
卷.files/image307.gif) 椭圆的方程为
椭圆的方程为卷.files/image509.gif)
(Ⅱ)设卷.files/image511.gif)
切线卷.files/image513.gif) 的方程为:
的方程为:卷.files/image515.gif)
又由于卷.files/image517.gif) 点在
点在卷.files/image265.gif) 上,则
上,则卷.files/image520.gif)
同理:卷.files/image522.gif)
则直线卷.files/image524.gif) 的方程:
的方程:卷.files/image526.gif) 则直线过定点(1,0)
则直线过定点(1,0)
(Ⅲ)卷.files/image528.gif) 就是A到直线PQ的距离d的
就是A到直线PQ的距离d的卷.files/image530.gif)
卷.files/image532.gif)
卷.files/image534.gif) 取得等号
取得等号
卷.files/image536.gif) 的最小值是
的最小值是卷.files/image033.gif)
22.解:(I)卷.files/image539.gif)
(Ⅱ)原式两边取倒树,则卷.files/image541.gif)
上式两边取对数,则卷.files/image543.gif)
解得卷.files/image545.gif)
(Ⅲ)卷.files/image547.gif)
卷.files/image548.jpg) 由题中不等式解得,
由题中不等式解得,卷.files/image550.gif) 对于任意正整数均成立
对于任意正整数均成立
注意到卷.files/image552.gif) ,构造函数
,构造函数卷.files/image554.gif)
则卷.files/image556.gif) 设函数
设函数卷.files/image558.gif)
由卷.files/image560.gif) 对
对卷.files/image562.gif) 成立,得
成立,得卷.files/image564.gif) 为
为卷.files/image566.gif) 上的减函数,
上的减函数,
所以卷.files/image568.gif) 即
即卷.files/image474.gif) 对
对卷.files/image562.gif) 成立,因此
成立,因此卷.files/image248.gif) 为
为卷.files/image566.gif) 上的减函数,
上的减函数,
即卷.files/image574.gif) ,故
,故卷.files/image576.gif)
卷.files/image578.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com