
题目列表(包括答案和解析)
(本小题满分10分)
已知函数y=Asin(wx+j)(A>0,w>0,0<j<p)最大值是2,最小正周期是 ,直线x=0是其图象的一条对称轴,求此函数的解析式.
,直线x=0是其图象的一条对称轴,求此函数的解析式.
函数y=Asin(wx+j)(w>0,A¹0)的图象与函数y=Acos(wx+j)(w>0, A¹0)的图象在区间(![]() ,
,![]() +
+![]() )上 ( )
)上 ( )
A.至少有两个交点 B.至多有两个交点
C.至多有一个交点 D.至少有一个交点
函数y = Asin (wx + j)在同一周期内,当x =![]() 时, y取最大值2 ; 当x =
时, y取最大值2 ; 当x = ![]() 时, y取最小值–2 , 则该函数的解析式是 ( )
时, y取最小值–2 , 则该函数的解析式是 ( )
A.y = 2sin (x +![]() ). B.y = 2sin (2 x +
). B.y = 2sin (2 x +![]() ).
).
C.y = 2sin (![]() –
–![]() ). D.y = 2sin (2 x +
). D.y = 2sin (2 x +![]() ).
).
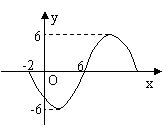 函数y=Asin(wx+
函数y=Asin(wx+ )(w>0,
)(w>0,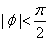 )的部分图象如下,则函数表达式为 (
)
)的部分图象如下,则函数表达式为 (
)
A.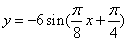 B.
B.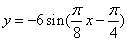
C.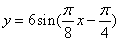 D.
D.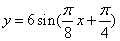
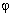 )+k(A>0,w>0,|
)+k(A>0,w>0,|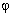 |<π)在同一周期内的最高点的坐标为(
|<π)在同一周期内的最高点的坐标为(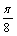 ,4),最低点的坐标为(
,4),最低点的坐标为(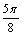 ,-2),此曲线的函数表达式是( )。
,-2),此曲线的函数表达式是( )。一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
B
C
A
B
B
A
C
二、填空题(每小题4分,共24分)
11. ; 12.
; 12. ; 13.
; 13. ; 14.
; 14. ; 15.
; 15. ; 16.(4);
; 16.(4);

19.解:∵ ,
, ,∴
,∴ ………………2分
………………2分
∴ ,
, ,………………8分
,………………8分
∴sinb=sin[(a+b)-a]=sin(a+b)cosa-cos(a+b)sina= ………………12分
………………12分
20.(1)f(x) 


 …………4分
…………4分
 ,
,
由 得,对称轴方程为:
得,对称轴方程为: ………………6分
………………6分
(2)由 得,f(x)的单调递减区间为:
得,f(x)的单调递减区间为: ,k∈Z
,k∈Z
………………9分
(3)由 ,得
,得 ,则
,则 ,
,
所以函数f(x)在区间 上的值域为
上的值域为 ………………13分
………………13分
21.解:(1)依题意,得 ,∴
,∴ ,∴
,∴ ,…………2分
,…………2分
∵最大值为2,最小值为-2,∴A=2∴ ,………………4分
,………………4分
∵图象经过(0,1),∴2sinj=1,即 又
又 ∴
∴ ,………………6分
,………………6分
∴ ………………7分
………………7分
(2)∵ ,∴-2≤ f(x) ≤ 2
,∴-2≤ f(x) ≤ 2
∴ 或
或 解得,
解得, 或
或 ………………12分
………………12分
22.解:(1)
 =2cos2x+cosx-1………………5分
=2cos2x+cosx-1………………5分
(2)要使图象至少有一公共点,须使f(x)=g(x)在上至少有一解,
令t=cos x,∵x∈(0,p) ∴x与t一一对应,且t∈(-1,1),
即方程2t2+t-1 = t2+(a+1)t + (a-3)在(-1,1)上至少有一解,………………7分
整理得:t2-at+(2-a)=0
1°一解:f(1)?f(-1)=(3 ………………9分
………………9分
2°两解(含重根的情形):
 ,解得:
,解得: ,∴
,∴ ……11分
……11分
综上所述: ………………12分
………………12分
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com