
题目列表(包括答案和解析)
( 14 分) 受轿车在保修期内维修费等因素的影响, 企业产生每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为 2 年,现从该厂已售出的两 种品牌轿车中随机抽取 50 辆,统计数据如下:

将频率视为概率,解答下列问题:
(I)从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;
(II)若该厂生产的轿车均能售出,记住生产一辆甲品牌轿车的利润为
 ,生产一辆乙品牌轿
车的利润为
,生产一辆乙品牌轿
车的利润为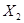 ,分别求
,分别求 ,
,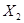 的分布列 ;
的分布列 ;
(III)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一 种品牌轿 车,若从经济效益的角度考虑,你认为应该产生哪种品牌的轿车?说明理由.
(本小题满分14分)
有一隧道既是交通拥挤地段,又是事故多发地段.为了保证安全,交通部门规定,隧道内的车距![]() 正比于车速
正比于车速![]() 的平方与车身长
的平方与车身长![]() 的积,且车距不得小于一个车身长
的积,且车距不得小于一个车身长![]() (假设所有车身长均为
(假设所有车身长均为![]() ).而当车速为
).而当车速为![]() 时,车距为1.44个车身长.
时,车距为1.44个车身长.
⑴求通过隧道的最低车速;
⑵在交通繁忙时,应规定怎样的车速,可以使隧道在单位时段内通过的汽车数量![]() 最多?
最多?
| 1 | 4 |
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
|
日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
【命题意图】本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率,是简单题.
【解析】(Ⅰ)当日需求量 时,利润
时,利润 =85;
=85;
当日需求量 时,利润
时,利润 ,
,
∴ 关于
关于 的解析式为
的解析式为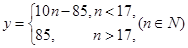 ;
;
(Ⅱ)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
 =76.4;
=76.4;
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为

已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当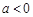 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com