
题目列表(包括答案和解析)
(本题满分12分)
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=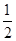 PD.
PD.
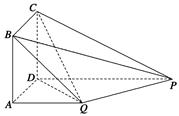
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q-BP-C的余弦值.
(本题满分12分)
如图所示,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.

(1)证明:PQ⊥平面DCQ;
(2)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
已知过抛物线y2=2px(p>0)的焦点,斜率为2![]() 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB![]() |=9.
|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若![]() =
=![]() +λ
+λ![]() ,求λ的值.
,求λ的值.
如图,在长方体ABCD—A1B1C1D1中,E,P分别是BC,A1D1的中点,M,N分别是AE,CD1的中点,AD=AA1=a,AB=2a.
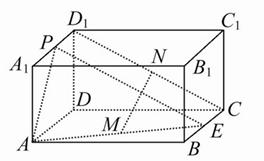
(1)求证:MN∥平面ADD1A1;
(2)求三棱锥P—DEN的体积.
(1)求点B的坐标;
(2)若直线l与双曲线C:![]() -y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
-y2=1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值;
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P 与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的 距离h关于t的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com