
题目列表(包括答案和解析)
(1)解不等式组.并把解集在数轴上表示出来. .
.
(2)阅读某同学解分式方程的具体过程,回答后面问题.
解方程 .
.
解:原方程可化为:
检验:当 时,各分母均不为0,
时,各分母均不为0,
∴ 是原方程的解.
是原方程的解. ⑤
⑤
请回答:(1)第①步变形的依据是____________________;
(2)从第____步开始出现了错误,这一步错误的原因是__________________________;
(3)原方程的解为____________________________.
(1)解不等式组.并把解集在数轴上表示出来.
 .
.
(2)阅读某同学解分式方程的具体过程,回答后面问题.
解方程 .
.
解:原方程可化为:

检验:当 时,各分母均不为0,
时,各分母均不为0,
∴ 是原方程的解.
是原方程的解. ⑤
⑤
请回答:(1)第①步变形的依据是____________________;
(2)从第____步开始出现了错误,这一步错误的原因是__________________________;
(3)原方程的解为____________________________.
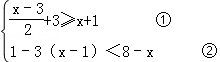 .
. .
.
 时,各分母均不为0,
时,各分母均不为0, 是原方程的解.
是原方程的解. ⑤
⑤| 900 |
| x+30 |
| 900 |
| x+30 |
| 600 |
| x |
| 600 |
| x |
| 900 |
| x+30 |
| 600 |
| x |
| 900 |
| x+30 |
| 600 |
| x |
注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可
1.如图①,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?

分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为![]() ,则每个竖彩条的宽为
,则每个竖彩条的宽为![]() .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形![]() .
.
2.结合以上分析完成填空:如图②,用含![]() 的代数式表示:
的代数式表示:
![]() =____________________________cm;
=____________________________cm;
![]() =____________________________cm;
=____________________________cm;
矩形![]() 的面积为_____________cm
的面积为_____________cm![]() ;
;
列出方程并完成本题解答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com