
题目列表(包括答案和解析)
(本题满分14分)
已知函数 的图象经过点
的图象经过点 和
和 ,记
,记
(1)求数列 的通项公式;
的通项公式;
(2)设 ,若
,若 ,求
,求 的最小值;
的最小值;
(3)求使不等式 对一切
对一切 均成立的最大实数
均成立的最大实数 .
.
(本题满分14分)
已知函数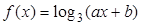 的图象经过点
的图象经过点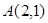 和
和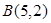 ,记
,记 (
(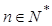 )
)
(1)求数列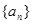 的通项公式;
的通项公式;
(2)设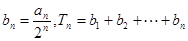 ,若
,若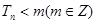 ,求
,求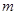 的最小值;
的最小值;
(3)求使不等式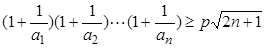 对一切
对一切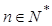 均成立的最大实数
均成立的最大实数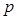 .
.
(本题满分14分)
已知函数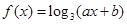 的图象经过点
的图象经过点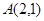 和
和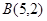 ,记
,记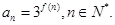
(1)求数列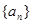 的通项公式;
的通项公式;
(2)设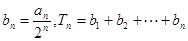 ,若
,若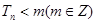 ,求
,求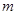 的最小值;
的最小值;
(3)求使不等式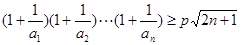 对一切
对一切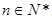 均成立的最大实数
均成立的最大实数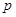 .
.
(本题满分14分)已知函数 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。
(1)求 的解析式;
的解析式;
(2)已知函数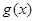 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得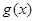 在
在 的值域也是
的值域也是 ,称区间
,称区间 为函数
为函数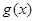 的“保值区间”.
的“保值区间”.
①当 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);
②当 时,问
时,问 是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
(本题满分14分)
已知函数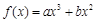 的图象经过点
的图象经过点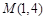 ,曲线在点
,曲线在点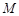 处的切线恰好与直线
处的切线恰好与直线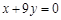 垂直.
垂直.
(1)求实数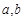 的值.
的值.
(2)若函数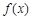 在区间
在区间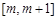 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
|