
题目列表(包括答案和解析)
(本题满分15分)已知函数![]()
![]() 且导数
且导数![]() .
.
(Ⅰ)试用含有![]() 的式子表示
的式子表示![]() ,并求
,并求![]() 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点![]() ,如果在函数图象上存在点
,如果在函数图象上存在点![]() (其中
(其中![]() )使得点
)使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数![]() 上是否存在两点
上是否存在两点![]() 、
、![]() 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出![]() 、
、![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本题满分15分)已知函数![]() 定义域为
定义域为![]() (
(![]() ),设
),设![]() .
.
(Ⅰ)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]()
![]()
![]() ,并确定这样的
,并确定这样的![]() 的个数 (其中
的个数 (其中![]() 为函数
为函数![]() 的导函数) .
的导函数) .
(本题满分15分)已知函数![]()
![]() .
.
(I)讨论![]() 在
在![]() 上的奇偶性;
上的奇偶性;
(II)当![]() 时,求函数
时,求函数![]() 在闭区间[-1,
在闭区间[-1,![]() ]上的最大值.
]上的最大值.
(本题满分15分)已知函数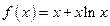 .
.
(1)求函数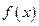 的图像在点
的图像在点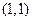 处的切线方程;
处的切线方程;
(2)若 ,且
,且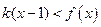 对任意
对任意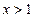 恒成立,求
恒成立,求 的最大值;
的最大值;
(3)当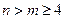 时,证明
时,证明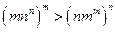 .
.
(本题满分15分)
已知函数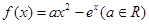 .
.
(Ⅰ)当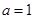 时,试判断
时,试判断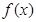 的单调性并给予证明;
的单调性并给予证明;
(Ⅱ)若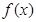 有两个极值点
有两个极值点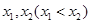 .
.
(i) 求实数a的取值范围;
(ii)证明: 。 (注:
。 (注: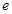 是自然对数的底数)
是自然对数的底数)
|