练习册

  • 练习册
  • 试题
    (1)若在y轴右侧加一平行于x轴的匀强电场.要使y轴右侧所有的运动粒子都能打到挡板MN上.则电场强度的最小值E0为多大?在电场强度为E0时.打到板上的粒子动能为多大?(2)若在整个空间加一方向垂直纸面向里的匀强磁场.要使该板右侧的MN连线上都有粒子打到.磁场的磁感应强度不能超过多少?若满足此条件.放射源O 向外发射出的所有带电粒子中有几分之几能打在板的左侧面上? 【查看更多】

     

    题目列表(包括答案和解析)

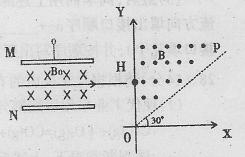
    如图所示，有一对平行金属板M、N垂直纸面放置，两板相距为d，板间电压为U，金属板M、N间有垂直纸面向里，磁感应强度为B0的匀强磁场；在平行金属板右侧有一平行纸面的直角坐标系XOY，坐标轴OY垂直于平行金属板，在其POY区域内有垂直纸面向外，磁感应强度为B的匀强磁场，磁场边界OP与X轴正方向夹角为30°；POX区域为无场区。一个带正电的粒子沿平行于金属板，垂直磁场方向射入两板间并做匀速直线运动，从H（0，h）点垂直于Y轴进入第I象限，经OP上某点离开磁场，最后沿与X轴正向成60°角的方向离开第I象限。求：

       （1）粒子在平行金属板间匀速运动的速率；

       （2）粒子的比荷；

       （3）若在POX区域加一个场强大小为E、方向与PO平行斜向下的匀强电场，使粒子刚好垂直于OX轴射出，其它条件不变，求粒子离开X轴的速度v以及在电场中运动的时间t．  

    查看答案和解析>>

    如图所示，有一对平行金属板M、N垂直纸面放置，两板相距为d，板间电压为U，金属板M、N间有垂直纸面向里，磁感应强度为B0的匀强磁场；在平行金属板右侧有一平行纸面的直角坐标系XOY，坐标轴OY垂直于平行金属板，在其POY区域内有垂直纸面向外，磁感应强度为B的匀强磁场，磁场边界OP与X轴正方向夹角为30°；POX区域为无场区。一个带正电的粒子沿平行于金属板，垂直磁场方向射入两板间并做匀速直线运动，从H（0，h）点垂直于Y轴进入第I象限，经OP上某点离开磁场，最后沿与X轴正向成60°角的方向离开第I象限。求：

       （1）粒子在平行金属板间匀速运动的速率；

       （2）粒子的比荷；

       （3）若在POX区域加一个场强大小为E、方向与PO平行斜向下的匀强电场，使粒子刚好垂直于OX轴射出，其它条件不变，求粒子离开X轴的速度v以及在电场中运动的时间t．  

    查看答案和解析>>

    如图(a)所示，建立xOy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，第一、四象限有一宽度一定的匀强磁场，磁感应强度为B，方向垂直于xOy平面向里。位于极板左侧的粒子源沿x轴向右连续发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~4t0时间内两板间加上如图(b)所示的电压（不考虑极板边缘的影响）。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、t、t0、B为已知量。（不考虑粒子间相互影响及返回板间的情况）
    （1）求两板间的电压U0；
    （2）0~t0时间内射入两板间的带电粒子都能够从磁场右边界射出，求磁场的最大宽度；
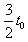    （3）时刻射入两板间的带电粒子进入磁场和离开磁场时的位置坐标；
    （4）若两板间电压为0，请设计一种方案：粒子源沿x轴向右连续发射的带电粒子，经过y轴右边的几个有边界的磁场后，带电粒子又返回粒子源。

    查看答案和解析>>

    如图所示，在坐标原点O处，能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子．在O点右侧有一半径为R的圆形薄板，薄板中心O′位于x轴上，且与x轴垂直放置，薄板的两端M、N与原点O正好构成等腰直角三角形．已知带电粒子的质量为m，带电量为q，速率为v，重力不计．
    （1）要使y轴右侧所有运动的粒子都能打到薄板MN上，可在y轴右侧加一平行于x轴的匀强电场，则场强的最小值E0为多大？在电场强度为E0时，打到板上的粒子动能为多大？
    （2）要使薄板右侧的MN连线上都有粒子打到，可在整个空间加一方向垂直纸面向里的匀强磁场，则磁场的磁感应强度不能超过多少（用m、v、q、R表示）？若满足此条件，从O点发射出的所有带电粒子中有几分之几能打在板的左边？

    查看答案和解析>>

    （18分）如图所示，在坐标原点O处，能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子。在O点右侧有一半径为R的圆形薄板，薄板中心O′位于x轴上，且与x轴垂直放置，薄板的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m，带电量为q，速率为v，重力不计。

    （1）要使y轴右侧所有运动的粒子都能打到薄板MN上，可在y轴右侧加一平行于x轴的匀强电场，则场强的最小值E0为多大？在电场强度为E0时，打到板上的粒子动能为多大?

    （2）要使薄板右侧的MN连线上都有粒子打到，可在整个空间加一方向垂直纸面向里的匀强磁场，则磁场的磁感应强度不能超过多少（用m、v、q、R表示）?若满足此条件，从O点发射出的所有带电粒子中有几分之几能打在板的左边?

    查看答案和解析>>

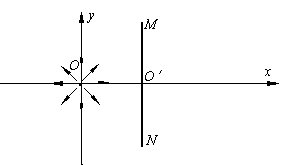
    一、1、CD 2、BD 3、D  4、AC 5、AD 6、AD  7、D 8、

    二、实验题：（18分）将答案填在题目的空白处，或者要画图连线。

    9、（8分）(1) 0.8462(0.8461~0.8464均可) （4分）(2)ABD（4分）

    10、（10分）⑵①BDE  ②如右图(各5分)

    三、本大题共三小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位  

    11、（16分））⑴滑块经过D点时做圆周运动，根据牛顿第二定律得：N－mg－Bqv1＝mv12/R（3分）

    解得：v1＝5m/s（2分）

    滑块从A滑到D点的过程中，系统在水平方向不受外力，故系统水平方向动量守恒，因此有：

    mv0＝mv1＋Mv2，解得：v2＝1m/s（2分）

    所以系统损失的机械能为：ΔE＝(mv02－mv12－Mv22)/2＝1.8（J）（2分）

    ⑵滑块经过D点时撤去磁场，滑块在圆弧轨道上往返运动过程，小车一直加速，当滑块滑过D点，相对小车向左运动时，小车做减速运动，所以滑块第二次经过D点时，小车速度最大，且为vm。根据水平方向系统动量守恒有：mv1+Mv2＝mv2+Mvm，（2分）由于相互作用过程没有能量损失，故系统动能也守恒，由动量守恒得：mv12+Mv22＝mv22+Mvm2

    由上面两式解得：v2＝－1m/s，vm＝3m/s。（3分）

    所以小车最大速度为3m/s。（2分）

    12、（18分）（１）由题意知，当加了电场后， y轴右侧的所有运动粒子将在电场力的作用下做类平抛运动，要使它们都能打在MN上，其临界条件为：沿y轴方向运动的粒子必须且只能落在M（沿y轴正向）点或N点（沿y轴负向）。由平抛运动规律有：

    ＭＯ´＝＝vt    （2分）

     OO´= tan450= at2      （2分）

     此时电场强度应为E0，由牛顿第二定律有qE0=ma     （2分）

    联立以上三式解得 E0=                     （1分）

    此过程电场力对粒子做正功，由动能定理知Ek=-+ qE0    （2分）

    即Ek=                        （1分）

    （2）此空间加上磁场后,所有粒子将在洛仑兹力的作用下,沿逆时针方向做匀速圆周运动, 由题设条件知，要使该板右侧的MN连线上都有粒子打到，粒子轨迹直径的最小值应为MN板的长度L，即R≥            （2分）

    当R=时,磁感应强度有最大值,设为B0.由R==得B0=        （2分）

    放射源O发射出的粒子中，在题设条件下，当B〈B0即R〉时，能打在板的左侧面上的粒子的临界径迹如右图所示。此时,沿x轴正向射出的粒子经磁偏转后刚好打到M点,沿y轴负向射出的粒子经磁偏转后刚好打到N点,则可知第四象限的粒子将全部分别打在MN上的其余各点上.

    ∴放射源O放射出的所有粒子中只有打在MN板的左侧。    （4分）

    13、（20分）⑴子弹进入小车的过程中，子弹与小车组成的系统动量守恒，由动量守恒定律得：

    m1v0＝(m2＋m1)v1    ①  （3分）

    由三物体组成的系统动量守恒，由动量守恒定律得：

    (m2＋m1)v1＝(m2＋m1＋m3)v2  ②  （3分）

    设小车最小长度为L，三物体相对静止后，对系统利用能量守恒定律得：

    (m2＋m1)v12－(m2＋m1＋m3)v22＝μm3gL    ③  （5分）

    联立以上方程解得：L＝0.9m   

    车与物体的共同速度为：v2＝2.1m/s (或m/s) （3分）

    ⑵以m3为研究对象，利用动量定理可得：μm3gt＝m3v2   ④（4分）

    解得：t＝0.52s(或s)   （2分）

     


    同步练习册答案