
题目列表(包括答案和解析)
已知函数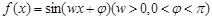 的周期为
的周期为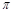 ,图象的一个对称中心为
,图象的一个对称中心为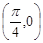 ,将函数
,将函数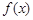 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个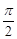 单位长度后得到函数
单位长度后得到函数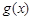 的图象。
的图象。
(Ⅰ)求函数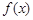 与
与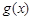 的解析式
的解析式
(Ⅱ)是否存在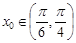 ,使得
,使得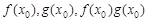 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定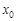 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(Ⅲ)求实数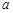 与正整数
与正整数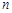 ,使得
,使得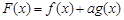 在
在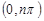 内恰有2013个零点
内恰有2013个零点
已知函数 的周期为
的周期为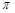 ,图象的一个对称中心为
,图象的一个对称中心为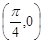 ,将函数
,将函数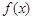 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个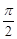 单位长度后得到函数
单位长度后得到函数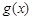 的图象。
的图象。
(Ⅰ)求函数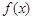 与
与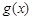 的解析式
的解析式
(Ⅱ)是否存在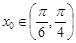 ,使得
,使得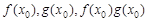 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定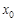 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(Ⅲ)求实数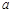 与正整数
与正整数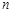 ,使得
,使得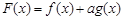 在
在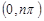 内恰有2013个零点
内恰有2013个零点
 的周期为
的周期为 ,图象的一个对称中心为
,图象的一个对称中心为 ,将函数
,将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数
单位长度后得到函数 的图象。
的图象。 与
与 的解析式
的解析式 ,使得
,使得 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定 的个数,若不存在,说明理由;
的个数,若不存在,说明理由; 与正整数
与正整数 ,使得
,使得 在
在 内恰有2013个零点
内恰有2013个零点若函数![]() 的图象的一个最高点为(2,
的图象的一个最高点为(2,![]() ),由这个最高点到相邻的最低点间的曲线与
),由这个最高点到相邻的最低点间的曲线与![]() 轴交于点(6,0)
轴交于点(6,0)
⑴求这个函数的解析式;
⑵求该函数的对称轴、对称中心、单调区间;
⑶这个函数怎样由![]() 进行变换得到?
进行变换得到?
设函数f(x)=x|x|+bx+c(b,c∈R),给出下列四个命题
①若c=0,则f(x)为奇函数;
②若b=0,c>0,则方程f(x)=0只有一个实根;
③函数y=f(x)的图象关于点(O,C)成中心对称图形;
④关于x的方程f(x)=0最多有两个实根.
其中正确的命题是________
一、选择题(每小题5分,共60分)
二、填空题(每小题4分,共16分)
13)5 14)2.6 15)48 16)①③④
三、解答题(本题共6小题,满分共74分)
17、解:(1)因为 。
。
所以1―2
 ……………2分
……………2分
所以
因为
所以  ……………………………6分
……………………………6分
(2) ……8分
……8分
因为
 …10分
…10分
所以,原式 ………………………12分
………………………12分
18、解:(Ⅰ)当n=1时, ………3分
………3分
(Ⅱ)(方法一)记输入n时,①中输出结果为 ,②中输出结果为
,②中输出结果为 ’则
’则
 ……………5分
……………5分
所以
 ……
…… ……
……
……………8分
(方法二)猜想 ……………5分
……………5分
证明:(1)当n=1时,结论成立
(2)假设当n=k
则当n=k+1时,

所以当 n=k+1时,结论成立
故对 ,都有
,都有 成立 ………………8分
成立 ………………8分
因为 ……………10分
……………10分
所以


 ……………………………12分
……………………………12分
19、解:(方法一)证明:设BD交AC于点O,连接MO,OF
因为四边形ABCD是正方形
所以AC⊥BD,AO=CO
又因为矩形ACEF,EM=FM,
所以MO⊥AO
因为正方形ABCD和矩形ACEF所
在平面垂直
平面ABCD 平面ACEF=AC
平面ACEF=AC
所以MO⊥平面ABCD
所以AM⊥BD
在 ,
,
所以BD=
所以AO=1,
所以四边形OAFM是正方形,所以AM⊥OF
因为 …………………6分
…………………6分
(Ⅱ)设AM、OF相交于Q,过A作AR⊥DF于R,连接QR,因为AM⊥平面BDF,
所以QR⊥DF,则∠ARQ为二面角A―DF―B的平面角…………………9分
Rt△ADF中,AF=1,AD= ,所以
,所以
Rt△AQR中,QR
所以二面角A―DF―B的余弦值为 ………………………12分
………………………12分
(方法二)以C为坐标原点建立如图所示的空间直角坐标系C―xyz,连接BD则A( ,
, ,0),B(0,
,0),B(0, ,0)。
,0)。
D( ,0,0)
,0,0)
F( ,
, ,1),M(
,1),M( ,
, ,1)
,1)
所以

所以

所以 所以AM⊥平面BDF…………6分
所以AM⊥平面BDF…………6分
(Ⅱ)平面ADF的法向量为
平面BDF的法向量 ………………8分
………………8分
 ……………………11分
……………………11分
所以二面角A―DF―B的余弦值为 。 ……………………12分
。 ……………………12分
20、解:设该人参加科目A考试合格和补考为时间 ,参加科目B考试合格和补考合格为时间
,参加科目B考试合格和补考合格为时间
 相互独立。
相互独立。
(Ⅰ)设该人不需要补考就可获得证书为事件C,则C=

(Ⅱ) 的可能取值为2,3,4.
的可能取值为2,3,4.
则P(
P
P …………………8分
…………………8分
所以,随即变量 的分布列为
的分布列为

2
3
4
P



所以 ………………12分
………………12分
21、解:(Ⅰ)设所求双曲线C的方程为 -
- =1,
=1,
由题意得:
所以,所求曲线C的方程为 ……………3分
……………3分
(Ⅱ)若弦PQ所在直线斜率K存在,则设其方程为y=k (x-2)
 由
由
设点P

解得
此时点R到y轴的距离
而当弦PQ所在直线的斜率不存在时,点R到Y轴的距离为2,
所以,点R到Y轴距离的最小值为2。 ………………8分
(Ⅲ)因为直线L:x=m与以PQ为直径的圆相切
所以 双曲线离心率e=
双曲线离心率e= ,右准线方程为
,右准线方程为
所以|PQ|=|PF|+|QF|=2

所以 ,所以
,所以
因为 ………………12分
………………12分
22、解:(1)因为
所以 
取BC的中点D,则
因为
所以,点0在BC边的中线上 ……………………………4分
(Ⅱ)因为 
所以
所以
所以
所以 ………………………………5分
………………………………5分
因为
又
=
所以  ……………………8分
……………………8分
因为
所以 …………………………………10分
…………………………………10分
(Ⅲ)由题意知

 在(0,+∞)上恒成立。
在(0,+∞)上恒成立。
令h(x)=
所以
所以h(x)在(0,+∞)内为增函数,所以 h(x)>h(0)=1 …………………13分
所以 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com