
题目列表(包括答案和解析)
如图所示,质量为0.05kg,长l=0.1m的铜棒,用长度也为l的两根轻软导线水平悬挂在竖直向上的匀强磁场中,磁感应强度为B=0.5T.不通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流多大?(不考虑棒摆动过程中产生的感应电流,g取10N/kg)
同学甲的解法如下:对铜棒受力分析如图所示:
当最大偏转角θ=37°时,棒受力平衡,有:
FTcosθ=mg,FTsinθ=F安=BIl
得I==A=7.5A
同学乙的解法如下:
F安做功:WF=Fx1=BIlsin37°×lsin37°=BI(lsin37°)2
重力做功:
WG=-mgx2=-mgl(1-cos37°)
由动能定理得:WF+WG=0
代入数据解得:I=A≈5.56A
请你对甲、乙两同学的解法作出评价:若你对两者都不支持,则给出你认为正确的解答.
如图所示,质量为0.05kg,长l=0.1m的铜棒,用长度也为l的两根轻软导线水平悬挂在竖直向上的匀强磁场中,磁感应强度为B=0.5T.不通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流多大?(不考虑棒摆动过程中产生的感应电流,g取10N/kg)
同学甲的解法如下:对铜棒受力分析如图所示:
当最大偏转角θ=37°时,棒受力平衡,有:
FTcosθ=mg,FTsinθ=F安=BIl
得I==A=7.5A
同学乙的解法如下:
F安做功:WF=Fx1=BIlsin37°×lsin37°=BI(lsin37°)2
重力做功:
WG=-mgx2=-mgl(1-cos37°)
由动能定理得:WF+WG=0
代入数据解得:I=A≈5.56A
请你对甲、乙两同学的解法作出评价:若你对两者都不支持,则给出你认为正确的解答.
如图所示,质量为0.05kg,长l=0.1m的铜棒,用长度也为l的两根轻软导线水平悬挂在竖直向上的匀强磁场中,磁感应强度为B=0.5T.不通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流多大?(不考虑棒摆动过程中产生的感应电流,g取10N/kg)
同学甲的解法如下:对铜棒受力分析如图所示:
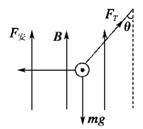
当最大偏转角θ=37°时,棒受力平衡,有:
FTcosθ=mg,FTsinθ=F安=BIl
得I==A=7.5A
同学乙的解法如下:
F安做功:WF=Fx1=BIlsin37°×lsin37°=BI(lsin37°)2
重力做功:
WG=-mgx2=-mgl(1-cos37°)
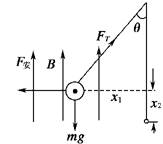
由动能定理得:WF+WG=0
代入数据解得:I=A≈5.56A
请你对甲、乙两同学的解法作出评价:若你对两者都不支持,则给出你认为正确的解答.
(A组)如图所示,定滑轮的半径r="2" cm,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2做匀加速运动,在重物由静止下落距离为1 m的瞬间,求滑轮边缘上的点的角速度和向心加速度。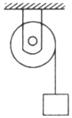
(B组)在竖直平面内有一个粗糙的1/4圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度H=0.8m。 一质量m=0.1kg的小滑块从轨道的最高点由静止释放,到达最低点时以一定的水平速度离开轨道。落地点距轨道最低点的水平距离S=0.8m。空气阻力不计,g取10 m/s2,求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到B点时,小球对轨道的压力多大?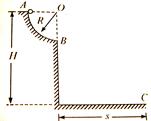
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com