练习册

  • 练习册
  • 试题
    (4)设二面角. 【查看更多】

     

    题目列表(包括答案和解析)

    设P(a,b)（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点(1,b)的直线，记Q是直线l与抛物线x2＝2py（p≠0）的异于原点的交点

    ⑴.已知a＝1，b＝2，p＝2，求点Q的坐标。

    ⑵.已知点P(a,b)（ab≠0）在椭圆+y2＝1上，p＝，求证：点Q落在双曲线4x2－4y2＝1上。

    ⑶.已知动点P(a,b)满足ab≠0，p＝，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由。

    查看答案和解析>>

    设平面直角坐标系中，设二次函数的图象与坐标轴有三个交点，经过这三个交点的圆记为C。

    （1）求实数的取值范围；

    （2）求圆的方程；

    （3）问圆是否经过某定点（其坐标与无关）？请证明你的结论。

    查看答案和解析>>

    设复数满足，且在复平面上对应的点在第二、四象限的角平分线上，若，求和的值。

    查看答案和解析>>

    设平面直角坐标系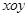中，设二次函数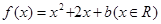的图象与坐标轴有三个交点，经过这三个交点的圆记为C。

    （1）求实数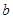的取值范围；

    （2）求圆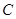的方程；

    （3）问圆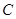是否经过某定点（其坐标与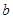无关）？请证明你的结论。

     

    查看答案和解析>>

    设P（a，b）（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点(1，b)的直线，记Q是直线l与抛物线x2=2py（p≠0）的异于原点的交点，
    （1）若a=1，b=2，p=2，求点Q的坐标；
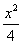    （2）若点P（a，b）（ab≠0）在椭圆+y2=1上，p=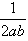，求证：点Q落在双曲线4x2-4y2=1上；
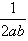    （3）若动点P(a，b)满足ab≠0，p=，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由。

    查看答案和解析>>

    一、选择题：本大题共10个小题，每小题5分，共50分．

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    C

    B

    C

    D

    C

    B

    A

    D

    B

    A

    二、填空题：本大题共4个小题，每小题4分，共16分．

    11.  630       12. 　2k   13.             14.   ①②③  

    三、解答题：本大题共6个小题，每小题14分，共84分．

    15．(4分)     

    由题意得  

    16． 有分布列：

    0

    1

    2

    3

    P

    从而期望

    17．（1）

           又

            

       (2)

          

          

       (3)DE//AB,

       (4)设BB1的中点为F，连接EF、DF，则EF是DF在平面BB1C1C上的射影。

         因为BB1C1C是正方形，

       

    18.(1) 由题意得　 

    (2)

    所以直线的斜率为

    令，则直线的斜率，                                       

    19．（1）由韦达定理得

    是首项为4，公差为2的等差数列。

    （2）由（1）知，则

    原式左边=

    ==右式。故原式成立。

     

    20．令x=y=0，有，令y=-x则得

    故（1）得证。

    　（2）在R上任取x1,x2且，且，

    　

    所以在R上单调递增；

    　（3）

    由得；

    由得；因为，

    所以无解，即圆心到直线的距离大于或等于半径2，只需

     

     


    同步练习册答案