
题目列表(包括答案和解析)
已知椭圆![]() 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点![]() ,点F2在线段PF1的中垂线上。
,点F2在线段PF1的中垂线上。
(1)求椭圆C的方程;(8分)
(2)设直线![]() 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标。(12分)
过定点,并求该定点的坐标。(12分)
已知椭圆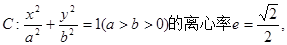 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点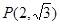 ,点F2在线段PF1的中垂线上.
,点F2在线段PF1的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为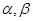 ,且
,且 ,求证:直线
,求证:直线 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知椭圆 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点 ,点F2在线段PF1的中垂线上.
,点F2在线段PF1的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为 ,且
,且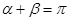 ,求证:直线
,求证:直线 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知椭圆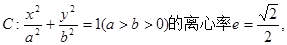 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,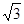 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
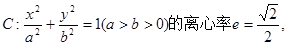 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,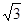 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.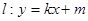 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
一、选择题:本大题共12个小题,每小题5分,共60分。
1―6BBCDBD 7―12CACAAC
二、填空题:本大题共4个小题,每小题4分,共16分。
13.0.8;(文)0.7
14.
15. ; (文)
; (文)
16.①③
三、解答题:
17.解:(1)由 ,
,
得

由正弦定得,得

又B

又
又 6分
6分
(2)
由已知
 9分
9分
当
因此,当 时,
时,

当 ,
,
 12分
12分
18.解:设“中三等奖”为事件A,“中奖”为事件B,
从四个小球中有放回的取两个共有(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)
(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的结果 3分
(1)两个小球号码相加之和等于4的取法有3种:
(1,3),(2,2),(3,1)
两个小球号相加之和等于3的取法有4种:
(0,3),(1,2),(2,1),(3,0) 4分
由互斥事件的加法公式得

即中三等奖的概率为 6分
6分
(2)两个小球号码相加之和等于3的取法有4种;
两个小球相加之和等于4的取法有3种;
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2)
两个小球号码相加之和等于6的取法有1种:(3,3) 9分
由互斥事件的加法公式得

|