
题目列表(包括答案和解析)
已知椭圆C的中心在坐标原点,长轴在x轴上,F1,F2分别为其左、右焦点,P为椭圆上任意一点,且![]() ·
·![]() 的最大值为1,最小值为-2.
的最大值为1,最小值为-2.
(1)求椭圆C的方程;
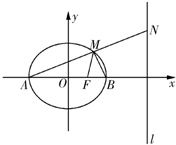
(2)设A为椭圆C的右顶点,直线l是与椭圆交于M,N两点的任意一条直线,若AM⊥AN,证明直线l过定点.
已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+![]() =0相切.
=0相切.
(1)求椭圆C的方程;
(2)设P(4,0),M、N是椭圆C上关于x轴对称的任意两个不同的点,连结PN交椭圆C于另一点E,求直线PN的斜率的取值范围;
(3)在(2)的条件下,证明直线ME与x轴相交于定点.
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| 16 |
| y2 |
| 12 |
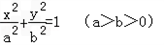 的左、右焦点,A、B分别为其左顶点和上顶点,△BF1F2是面积为
的左、右焦点,A、B分别为其左顶点和上顶点,△BF1F2是面积为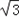 的正三角形.
的正三角形.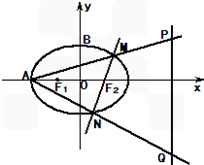
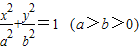 的左、右焦点,A、B分别为其左顶点和上顶点,△BF1F2是面积为
的左、右焦点,A、B分别为其左顶点和上顶点,△BF1F2是面积为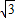 的正三角形.
的正三角形.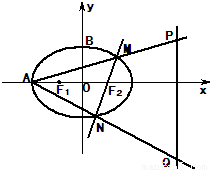
一、选择题:本大题共12个小题,每小题5分,共60分。
1―6BBCDBD 7―12CACAAC
二、填空题:本大题共4个小题,每小题4分,共16分。
13.0.8;
14.
15. ;
;
16.①③
三、解答题:
17.解:(1)由 ,
,
得

由正弦定得,得

又B

又
又 6分
6分
(2)
由已知
 9分
9分
当
因此,当 时,
时,

当 ,
,
 12分
12分
18.解:(1)依题意,甲答对主式题数 的可能取值为0,1,2,3,则
的可能取值为0,1,2,3,则



 4分
4分
 的分布列为
的分布列为

0
1
2
3
P




甲答对试题数 的数学期望为
的数学期望为
 6分
6分
(2)设甲、乙两人考试合格的事件分别为A、B,则

 9分
9分
因为事件A、B相互独立,
 甲、乙两人考试均不合格的概率为
甲、乙两人考试均不合格的概率为

 甲、乙两人至少有一人考试合格的概率为
甲、乙两人至少有一人考试合格的概率为

答:甲、乙两人于少有一人考试合格的概率为 12分
12分
另解:甲、乙两人至少有一个考试合格的概率为

答:甲、乙两人于少有一人考试合格的概率为
19.解法一(1)过点E作EG 交CF于G,
交CF于G,
|