
题目列表(包括答案和解析)
(本小题满分12分)过椭圆 引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
(1)若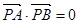 ,求P点坐标;
,求P点坐标;
(2)求直线AB的方程(用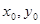 表示);
表示);
(3)求△MON面积的最小值.(O为原点)
(本小题满分16分)甲、乙两人各进行3次射击,甲每次击中目标的概率为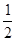 ,乙每次击中目标的概率为
,乙每次击中目标的概率为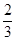 .
.
(1)记甲击中目标的次数为X,求X的概率分布及数学期望E (X);
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.
(本小题满分16分)过原点O作圆x2+y2-8x=0的弦OA。
(1) 求弦OA中点M的轨迹方程;
(2)如点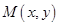 是(1)中的轨迹上的动点,
是(1)中的轨迹上的动点,
①求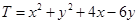 的最大、最小值;
的最大、最小值;
②求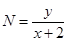 的最大、最小值。
的最大、最小值。
(本小题满分16分)已知椭圆 中心为
中心为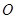 ,右顶点为
,右顶点为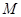 ,过定点
,过定点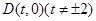 作直线
作直线 交椭圆于
交椭圆于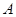 、
、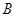 两点.
两点.
(1)若直线 与
与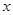 轴垂直,求三角形
轴垂直,求三角形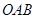 面积的最大值;
面积的最大值;
(2)若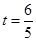 ,直线
,直线 的斜率为
的斜率为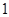 ,求证:
,求证: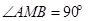 ;
;
(3)在 轴上,是否存在一点
轴上,是否存在一点 ,使直线
,使直线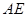 和
和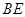 的斜率的乘积为非零常数?若存在,求出点
的斜率的乘积为非零常数?若存在,求出点 的坐标和这个常数;若不存在,说明理由.
的坐标和这个常数;若不存在,说明理由.
(文科做)(本小题满分16分)
已知椭圆 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 上任一点
上任一点 作圆
作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)求椭圆的方程;
(2)若直线 与圆
与圆 的另一交点为
的另一交点为 ,当弦
,当弦 最大时,求直线
最大时,求直线 的直线方程;
的直线方程;
(3)求 的最值.
的最值.
一、填空题:
1、 2、(1.5,0)
3、
2、(1.5,0)
3、 4、95%
4、95%
5、 6、大前提 7、18
6、大前提 7、18
8、4 9、 10、4 11、
10、4 11、 12、
12、 13、②③ 14、
13、②③ 14、
二、解答题:
15. (14分) 解:设 ,而
,而 即
即
则

16、(14分)解: 一般性的命题为
证明:左边

晕机
不晕机
合计
男
24
31
55
女
8
26
34
合计
32
57
89
所以左边等于右边
17、(15分).根据题意,列出列联表如下:
提出统计假设, :在恶劣气候飞行中男人与女人一样容易晕机则
:在恶劣气候飞行中男人与女人一样容易晕机则

 ,故我们有90%的把握认为在这次航程中男人比女人更容易晕机.
,故我们有90%的把握认为在这次航程中男人比女人更容易晕机.
18、(15分)解: (1) 散点图略
(2) 



 ;
; 
所求的回归方程为 
(3) 当 ,
, 
预测生产100吨甲产品的生产能耗比技改前降低 (吨)
(吨)
19、(16分)解:(I)由函数的图像经过点(0,2)可知, ,
,
 ,∵
,∵ 在点M(-1,f(-1))处的切线方程为
在点M(-1,f(-1))处的切线方程为 .
.
 ,
,
(II)


20、(14分)解:(1) ∴OAPB的正方形
∴OAPB的正方形
由
 ∴P点坐标为(
∴P点坐标为( )
)
(2)设A(x1,y1),B(x2,y2)
则PA、PB的方程分别为 ,而PA、PB交于P(x0,y0)
,而PA、PB交于P(x0,y0)
即x1x0+y1y0=4,x2x0+y2y0=4,∴AB的直线方程为:x0x+y0y=4
(3)由 、
、



当且仅当 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com