选考题：从以下3题中选择2题做答，每题7分，若3题全做，则按前2题给分。

(1)（选修4—2   矩阵与变换）（本题满分7分）

变换是将平面上每个点的横坐标乘2，纵坐标乘4，变到点。

（Ⅰ）求变换的矩阵；

（Ⅱ）圆在变换的作用下变成了什么图形？

(2)（选修4—4 参数方程与极坐标）（本题满分7分）

在极坐标系下，已知圆O：和直线，

（Ⅰ）求圆O和直线的直角坐标方程；

（Ⅱ）当时，求直线与圆O公共点的一个极坐标.

(3)（选修4—5  不等式证明选讲）（本题满分7分）

对于任意实数和，不等式恒成立，试求实数的取值范围．

（本小题满分12分）

已知点，过点作抛物线的切线，切点在第二象限，如图．

（Ⅰ）求切点的纵坐标；

（Ⅱ）若离心率为的椭圆  恰好经过切点，设切线交椭圆的另一点为，记切线的斜率分别为，若，求椭圆方程．

21（本小题满分12分）

已知函数 _.

（1）讨论函数的单调性；

（2）当时，恒成立，求实数的取值范围；

（3）证明：.

22．选修4－1：几何证明选讲

如图，是圆的直径，是弦，的平分线交圆于点，，交的延长线于点，交于点。

（1）求证：是圆的切线；

（2）若，求的值。

23.选修4—4：坐标系与参数方程

在平面直角坐标系中，直线过点且倾斜角为，以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为，直线与曲线相交于两点；

（1）若，求直线的倾斜角的取值范围；

（2）求弦最短时直线的参数方程。

24． 选修4-5 不等式选讲

已知函数

   （I）试求的值域；

   （II）设，若对，恒有成立，试求实数a的取值范围。

(本小题满分16分)

按照某学者的理论，假设一个人生产某产品单件成本为元，如果他卖出该产品的单价为元，则他的满意度为；如果他买进该产品的单价为元，则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为和，则他对这两种交易的综合满意度为.

现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为元和元，甲买进A与卖出B的综合满意度为，乙卖出A与买进B的综合满意度为

(1)求和关于、的表达式；当时，求证：=；

(2)设，当、分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？ (3)记(2)中最大的综合满意度为，试问能否适当选取、的值，使得和同时成立，但等号不同时成立？试说明理由。

(本小题满分16分)

按照某学者的理论，假设一个人生产某产品单件成本为元，如果他卖出该产品的单价为元，则他的满意度为；如果他买进该产品的单价为元，则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为和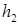，则他对这两种交易的综合满意度为.

现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为元和元，甲买进A与卖出B的综合满意度为，乙卖出A与买进B的综合满意度为

(1)求和关于、的表达式；当时，求证：=；

(2)设，当、分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？ (3)记(2)中最大的综合满意度为，试问能否适当选取、的值，使得和同时成立，但等号不同时成立？试说明理由。