在平面直角坐标系xoy中，已知曲线C₁：x²+y²=1，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ(2cosθ-sinθ)=6.

（Ⅰ）将曲线C₁上的所有点的横坐标，纵坐标分别伸长为原来的、2倍后得到曲线C₂，试写出直线l的直角坐标方程和曲线C₂的参数方程.

（Ⅱ）在曲线C₂上求一点P，使点P到直线l的距离最大，并求出此最大值．

【解析】（Ⅰ）根据极坐标与普通方程的互化，将直线l：ρ(2cosθ-sinθ)=6化为普通方程，C₂的方程为，化为普通方程；（Ⅱ）利用点到直线的距离公式表示出距离，求最值.

 

已知C₁的极坐标方程为ρcos(θ-

π

4

)=1，M，N分别为C₁在直角坐标系中与x轴，y轴的交点．曲线C₂的参数方程为

x= t - 1 t y=4-(t+ 1 t )

（t为参数，且t＞0），P为M，N的中点．
（1）将C₁，C₂化为普通方程；
（2）求直线OP（O为坐标原点）被曲线C₂所截得弦长．

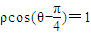已知C₁的极坐标方程为，M，N分别为C₁在直角坐标系中与x轴，y轴的交点．曲线C₂的参数方程为（t为参数，且t＞0），P为M，N的中点．
（1）将C₁，C₂化为普通方程；
（2）求直线OP（O为坐标原点）被曲线C₂所截得弦长．

选修4—4：坐标系与参数方程

已知曲线Ｃ₁的极坐标方程为,曲线C₂的极坐标方程为，曲线C₁,C₂相交于点A、B．

    (1)分别将曲线C₁，C₂的极坐标方程化为直角坐标方程；

    (2)求弦AB的长．