
题目列表(包括答案和解析)
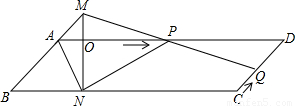 已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)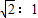 的两部分?若存在,求出相应的t值;若不存在,说明理由.
的两部分?若存在,求出相应的t值;若不存在,说明理由.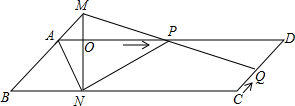 (2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
(2013•青岛)已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)| 2 |
为了调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了 8名学生,他们每天完成作业所需时间(单位:分)分别为:60,55,75,55,55,43,65,40。
(1)这组数据的众数是_______分、中位数是______分。
(2)求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过60分钟,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?
四.解答下列各题(每小题7分,共14分)
![]() 如图,已知在 ABCD中,E、F 是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、HG。
如图,已知在 ABCD中,E、F 是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、HG。
求证:四边形是平行四边形

已知,如图, ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
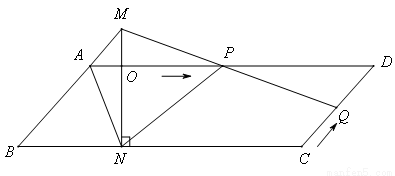
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是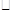 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成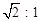 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
已知,如图, ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
一、BACBB CDCCA
二、11.答案不唯一,如: ,π,0.1010010001… 12.
,π,0.1010010001… 12. 
13.3,90 14. 2 15.15 16.菱形 17.24 18. 60°
15.15 16.菱形 17.24 18. 60°
三、19. (m)
(m)
20.(1)原式= …………………………………………
2分
…………………………………………
2分
= ………………………………………… 3分
………………………………………… 3分
当 时,
时,
原式= ………………………………… 4分
………………………………… 4分
=1-1+4
=4. ………………………………………… 5分
(2)原式= …………………………………… 1分
…………………………………… 1分
= ………………………………………… 2分
………………………………………… 2分
= ………………………………………… 3分
………………………………………… 3分
当 时,
时,
原式= ………………………………………… 4分
………………………………………… 4分
= .
………………………………………… 5分
.
………………………………………… 5分
21.(1)原式=3(a2-8a+16) ………………………………………… 2分
=3(a-4)2. ………………………………………… 5分
(2)原式=m2+m-4m-4+3m ………………………………………… 2分
=m2-4 ………………………………………… 3分
=(m+2)(m-2). ………………………………………… 5分
22. 正确画△A1B1C1给3分,正确画△A2B2C2给3分,共6分.
23. 在 ABCD中,AB=DC,AD=BC.
………………………………………… 2分
ABCD中,AB=DC,AD=BC.
………………………………………… 2分
∴ AB+AD= .
………………………………………… 3分
.
………………………………………… 3分
∵ AD=2AD,
∴ 2AD+AD=12. ………………………………………… 4分
∴ AD=4,BC=4. ………………………………………… 6分
AB=DC=8. ………………………………………… 7分
24. △OAB是等边三角形的理如下:
在矩形ABCD中,OA=0C,OB=OD, ………………………………………… 2分
AC=BD, ………………………………………… 4分
∴ OA= AC,OB=
AC,OB= BD.
………………………………………… 6分
BD.
………………………………………… 6分
又∵ AB= AC,
AC,
∴ OA=OB=AB.
即△OAB是等边三角形. ………………………………………… 7分
25. (1)在 ABCD中,∠DAB+∠ABC=180°,………………………………………… 2分
ABCD中,∠DAB+∠ABC=180°,………………………………………… 2分
∵ AE,BF分别平分∠DAB和∠ABC,
∴ ∠EAB+∠FBA=90°, ………………………………………… 3分
∴ AE⊥BF. ………………………………………… 4分
(2)在 ABCD中,DA=CB,DC∥AB, ………………………………………… 6分
ABCD中,DA=CB,DC∥AB, ………………………………………… 6分
∴ ∠EAB=∠DEA, ………………………………………… 7分
∵ ∠DAE=∠EAB,
∴ ∠DAE=∠DEA, ………………………………………… 8分
∴DA=DE. ………………………………………… 9分
同理,得 CF=CB. ………………………………………… 10分
∴ DE=CF, ………………………………………… 11分
∴ DE-FE=CF-FE,
即 DF=CF. ………………………………………… 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com