练习册

  • 练习册
  • 试题
    对于题目“如图1.在一个直角三角形的内部作矩形ABCD.其中AB和AD在两直角边上.设.矩形ABCD的面积为.当X取何值时.Y的值最大?最大值是多少? (答案是当X=20时.Y的值最大.最大值是300).小华同学提出了如下两个问题.你能帮助他解决吗?如果按图2 【查看更多】

     

    题目列表(包括答案和解析)

    对于题目“如图1，在一个直角三角形的内部作矩形ABCD，其中AB和AD在两直角边上，设AB=xcm，矩形ABCD的面积为ycm2，当x取何值时，y的值最大，最大值是多少？”（答案是当x=20时，y的值最大，最大值是300）．小华同学提出了如下两个问题，你能帮助他解决吗？
    如果按图2使矩形的一边BC在斜边EF上，如何解答此时求出来的最大值仍是300cm2吗？你能肯定图1和图2中的两个面积最大的矩形全等吗？请说明理由．
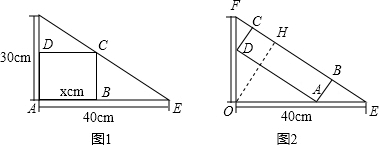
    精英家教网

    查看答案和解析>>

    如图1，过△ABC顶点A作BC边上的高AD和中线AE，点D是垂足，点E是BC中点，规定λA=
    DEBE
    ．特别地，当D、E重合时，规定λA=0．另外对λB、λC也作类似规定．

    （1）①当△ABC中，AB=AC时，则λA=
    0
    0
    ；②当△ABC中，λA=λB=0时，则△ABC的形状是
    等边三角形
    等边三角形
    ；
    （2）如图2，在Rt△ABC中，∠A=30°，求λA和λC的值；
    （3）如图3，正方形网格中，格点△ABC的λA=
    2
    2
    ；
    （4）判断下列三种说法的正误（正确的打“√”错误的打“×”）
    ①若△ABC中λA＜1，则△ABC为锐角三角形
    ×
    ×
    ；
    ②若△ABC中λA=1，则△ABC为直角三角形
    √
    √
    ；
    ③若△ABC中λA＞1，则△ABC为钝角三角形
    √
    √
    ；
    （5）通过本题解答，同学们应该有这样的认识：一个无论多么陌生、多么综合的问题，其实都来自于书本已学的基础知识．因此，我们今后应重视基础知识的学习；同时在解决问题时或者解决问题后，应该思考该问题的本质和目的：①巩固哪些基础知识；②培养我们哪些方面能力；③向我们渗透哪些数学思想．本题之所以是一道综合题，就是因为涉及到的知识点多、面广．下面就请你谈谈本题中所用到的、已学过的性质、定理、公理或判定等．（至少列举两条）

    查看答案和解析>>

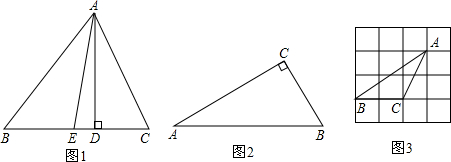
    在一节数学课上，老师要求同学们练习一道题，题目的图形如图所示，图中的BD是∠ABC的平分线，在同学们忙于画图和分析题目时，小明同学忽然兴奋地大声说：“我有个发现！”原来他感到自己创造了一个在直角三角形中画锐角的平分线的方法，他的方法是这样的，在AB上取点E，使BE＝BC，然后画DE⊥AB交AC于D，那么BD就是∠ABC的平分线．

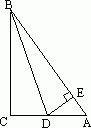
    有的同学对小明的画法表示怀疑，你认为他的画法对不对呢？请说明理由．

    查看答案和解析>>

    如图(a)，已知直线EA与两坐标轴轴分别交于点E、A(0,2)，过直线EA上的两个点F、G分别作轴的垂线，垂足分别为M(m，0)、N(n，0)，其中m＜0，n＞0．

    (1)

    如果m=－4，n=1，试计算线段AN和AM的长，并判断△AMN的形状；

    (2)

    如果mn=－4，(1)中有关△AMN的形状的结论还成立吗？如果成立，请证明；如果不成立，请说明理由；

    (3)

    如图(b)，题目中的条件不变，如果mn=－4，并且ON=4，求经过M、A、N三点的抛物线方程；

    (4)

    在(3)中，如果抛物线的对称轴与线段AN交于点P，点Q是对称轴上一动点，以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似，求符合条件的Q点坐标．

    查看答案和解析>>

    （2009•兖州市模拟）对于题目“如图1，在一个直角三角形的内部作矩形ABCD，其中AB和AD在两直角边上，设AB=x cm，矩形ABCD的面积为ycm2，当x取何值时，y的值最大，最大值是多少？”（答案是当x=20时，y的值最大，最大值是300）．小华同学提出了如下两个问题，你能帮助他解决吗？
    如果按图2使矩形的一边BC在斜边EF上，如何解答此时求出来的最大值仍是300cm2吗？你能肯定图1和图2中的两个面积最大的矩形全等吗？请说明理由．

    查看答案和解析>>


    同步练习册答案