
题目列表(包括答案和解析)
(本题满分10分)甲乙两地相距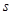 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过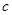 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度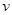 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为 ,固定部分为
,固定部分为 元.
元.
(1)把全程运输成本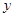 (元)表示为
(元)表示为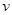 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(本题满分10分)已知二次函数![]() ,
,![]() ,
,
![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,若
,若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数![]() 的取值范围.
的取值范围.
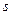 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过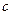 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度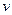 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为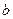 ,固定部分为
,固定部分为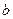 元.
元.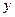 (元)表示为
(元)表示为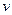 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;(本题满分10分)甲乙两地相距![]() km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过![]() km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元.
元.
(1)把全程运输成本![]() (元)表示为
(元)表示为![]() 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
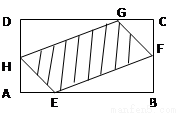
(本题满分10分) 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=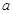 (
(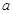 >2),BC=2,且AE=AH=CF=CG,
>2),BC=2,且AE=AH=CF=CG,
设AE=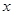 ,绿地面积为
,绿地面积为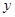 .
.
(1)写出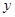 关于
关于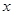 的函数关系式,并指出这个函数的定义域;
的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积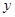 最大?
最大?
一. 选择题:(本大题共10道小题,每小题3分,共30分)
1
2
3
4
5
6
7
8
9
10
B
B
D
B
A
C
C
D
B
C
二.填空题:(本大题共5道小题,每小题4分,共20分)
11..files/image161.gif) 12.
12. .files/image163.gif) 13. 3 14.(0,+
13. 3 14.(0,+.files/image165.gif) ) 15.
) 15. .files/image167.gif)
三. 解答题: (本大题共6道小题,满分50分)
16.(1)原式=.files/image169.gif) ………2分
………2分
.files/image171.gif) …………………………………2分
…………………………………2分
(2).files/image173.gif)
.files/image175.gif) …………2分
…………2分
.files/image177.gif) ,从而
,从而.files/image179.gif) .
.
.files/image181.gif) …………………………………………………………2分
…………………………………………………………2分
17. (1) 当.files/image136.gif) 时
时
.files/image184.gif) ,
,.files/image186.gif) ;
;
.files/image188.gif) ………………………………………………………4分
………………………………………………………4分
(2)若.files/image140.gif) ,则或者
,则或者.files/image190.gif) 或者
或者.files/image192.gif) .
.
当.files/image190.gif) 时,有
时,有 .files/image194.gif) ,得
,得.files/image196.gif) ;
;
当.files/image192.gif) 时,有
时,有 .files/image199.gif) ,且
,且.files/image201.gif) .
.
得.files/image142.gif) 不存在;
不存在;
故实数.files/image204.gif) ……………………………………………………………4分
……………………………………………………………4分
18.
由已知得.files/image206.gif) ……………………………………3分
……………………………………3分
或.files/image208.gif) …………………………………………3分
…………………………………………3分
解得.files/image210.gif) 或
或.files/image212.gif) ,故函数
,故函数.files/image156.gif) 的零点为-2,1……………2分
的零点为-2,1……………2分
19.令.files/image215.gif) ,则
,则.files/image217.gif) .
.
.files/image219.gif) ,即
,即.files/image221.gif) ;3分
;3分
.files/image223.gif) ,即
,即.files/image225.gif) .3分
.3分
.files/image227.gif) ……………………………………………………………2分
……………………………………………………………2分
20.(1)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,
则.files/image229.gif)
.files/image231.gif) ………2分
………2分
∵k<0,∴x=200时,ymax= - 10000k,
即商场要获取最大利润,羊毛衫的标价应定为每件200元. …………………2分
(2)由题意得,k?(x- 100)?(x- 300)= - 10000k?75%.........2分
.files/image233.gif)
.files/image235.gif)
所以,商场要获取最大利润的75%,每件标价为250元或150元……………2分
21.解:(1)因为.files/image156.gif) 是奇函数,所以
是奇函数,所以.files/image238.gif) ,
,
即.files/image240.gif)
又由f(1)= -f(-1)知.files/image242.gif) ………………………2分
………………………2分
(2)由(1)知.files/image244.gif) ,
,
任取.files/image246.gif) ,则
,则
.files/image248.gif)
因为.files/image250.gif)
.files/image252.gif) 故
故.files/image254.gif) ,又
,又.files/image256.gif) ,从而
,从而
.files/image258.gif) ,即
,即.files/image260.gif)
.files/image262.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com