
题目列表(包括答案和解析)
(本小题满分12分)
阅读下面内容,思考后做两道小题。
在一节数学课上,老师给出一道题,让同学们先解,题目是这样的:
已知函数f(x)=kx+b,1≤f(1)≤3,-1≤f(-1)≤1,求Z=f(2)的取值范围。
题目给出后,同学们马上投入紧张的解答中,结果很快出来了,大家解出的结果有很多个,下面是其中甲、乙两个同学的解法:
甲同学的解法:由f(1)=k+b,f(-1)=-k+b得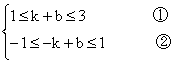
①+②得:0≤2b≤4,即0≤b≤2 ③
② ×(-1)+①得:-1≤k-b≤1 ④
④+②得:0≤2k≤4 ⑤
③+⑤得:0≤2k+b≤6。
又∵f(2)=2k+b
∴0≤f(2)≤6,0≤Z≤6
乙同学的解法是:由f(1)=k+b,f(-1)=-k+b得
①+②得:0≤2b≤4,即:0≤b≤2 ③
①-②得:2≤2k≤2,即:1≤k≤1
∴k=1,
∵f(2)=2k+b=1+b
由③得:1≤f(2)≤3
∴:1≤Z≤3
(Ⅰ)如果课堂上老师让你对甲、乙两同学的解法给以评价,你如何评价?
(Ⅱ)请你利用线性规划方面的知识,再写出一种解法。
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为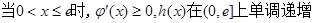 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
设函数f(x)= 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(1)求正实数a的取值范围;
(2)比较 的大小,说明理由;
的大小,说明理由;
(3)求证: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一问中,利用
解:(1)由已知: ,依题意得:
,依题意得: ≥0对x∈[1,+∞
≥0对x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0对x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
∴n≥2时:f( )=
)=
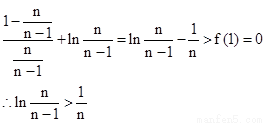
(3) ∵ ∴
∴
(本小题满分12分)已知f (x)=(1+x)m+(1+2x)n(m,n∈N*)的展开式中x的系数为11.
(1)求x2的系数的最小值;
(2)当x2的系数取得最小值时,求f (x)展开式中x的奇次幂项的系数之和.
解: (1)由已知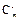 +2
+2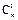 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为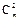 +22
+22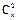 =
=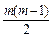 +2n(n-1)=
+2n(n-1)=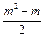 +(11-m)(
+(11-m)(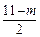 -1)=(m-
-1)=(m-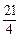 )2+
)2+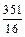 .
.
∵m∈N*,∴m=5时,x2的系数取最小值22,此时n=3.
(2)由(1)知,当x2的系数取得最小值时,m=5,n=3,
∴f (x)=(1+x)5+(1+2x)3.设这时f (x)的展开式为f (x)=a0+a1x+a2x2+…+a5x5,
令x=1,a0+a1+a2+a3+a4+a5=25+ 33,
33,
令x=-1,a0-a1+a2-a3+a4-a5=-1,
两式相减得2(a1+a3+a5)=60, 故展开式中x的奇次幂项的系数之和为30.
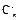 +2
+2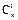 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为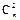 +22
+22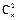 =
=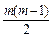 +2n(n-1)=
+2n(n-1)=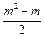 +(11-m)(
+(11-m)(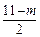 -1)=(m-
-1)=(m-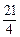 )2+
)2+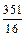 .
. 33,
33,湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com