
题目列表(包括答案和解析)
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
| |PF1-PF2| |
| |OP| |
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
| |PF1-PF2| |
| |OP| |
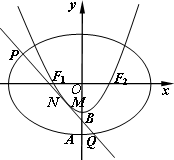 设椭圆C1:
设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 5 |
设椭圆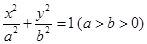 的左、右顶点分别为
的左、右顶点分别为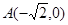 、
、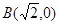 ,离心率
,离心率 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线MN过椭圆的右焦点与椭圆相交于M、N两点,且 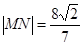 ,求直线MN的方程.
,求直线MN的方程.
一.选择题
BADCC ACCCC AD
二.填空题
13. 14. 29 15.
14. 29 15. (开闭区间均可) 16. ①
④
(开闭区间均可) 16. ①
④
三、解答题
17.解:
(1)∵ , ∴
, ∴ ,
,
即 ………3分
………3分
则  .
. , ∴
, ∴ ………6分
………6分
(2)由题知 ,得
,得 ,
, ………8分
………8分
得sinB=2cosB, ………10分
………10分
∴



 ………12分
………12分
18.解:
(1)得分为60分,12道题必须全做对。在其余的5道题中,有两道题答对的概率为 ,
,
有一道题答对的概率为 ,还有两道答对的概率为
,还有两道答对的概率为 ………2分
………2分
所以得分为60分的概率为:P= ………4分
………4分
(2)由 可得
可得 ………5分
………5分
得 ,得2<x<15,则x=5或x=10,则相应得分为55分或50分……7分
,得2<x<15,则x=5或x=10,则相应得分为55分或50分……7分
得分为50分表示只做对了10道题,做错2道题,所以概率为

 +
+
+ =
= ………9分
………9分
得分为55分表示只做对了11道题,做错1道题,所以概率为:
P2= =
= ………11分
………11分
则所求概率为 +
+ =
= 。答:该考生得分的概率为
。答:该考生得分的概率为 ………12分
………12分
19.证明:
(1)面A1B
又 面AB
B
(2)由于BC⊥面AB
又 AB
AB ,则AH=
,则AH= 为A到平面VBC的距离………7分
为A到平面VBC的距离………7分
(3)过H作HG⊥VB于G,连AG则∠AGH为二面角A-VB-C的平面角
在Rt B1CB中
B1CB中 ………10分
………10分
又Rt B1HG∽Rt
B1HG∽Rt B1BC 则
B1BC 则 ,即
,即
 故二面角A-VB-C的大小为
故二面角A-VB-C的大小为 ………12分
………12分
(本题也可用建立空间直角坐标系然后用空间向量求解,评分标准参照执行)
20.解:
(1)设{an}的公差d,为{bn}的公比为q,则

 ………6分
………6分
(2){Cn}的前n-1项中共有{an}中的1+2+3+…(n-1)= 个项………8分
个项………8分
且{an}的第 项为
项为 ………10分
………10分
故Cn是首项为 ,公差为2,项数为n的等差数列的前n项和,
,公差为2,项数为n的等差数列的前n项和,
 ………12分
………12分
21.解:
(1)f‘(x)=x2+ax+b,由 f‘(3)=9+
(2)令f‘(x)= x2+ax
当a=-6时,f‘(x)= ≥0,则f(x)无单调递减区间………4分
≥0,则f(x)无单调递减区间………4分
当a>-6时,令f‘(x) =(x-3)(x+a+3)≤0,得-a-3≤x≤3,
则f(x)的单调递减区间为[-a-3,3] ………6分
当a<-6时,易得f(x)的单调递减区间为[3,-a-3]
综上所述当a=-6时, f(x)无单调递减区间;当a>-6时,f(x)的单调递减区间为[-a-3,3],
当a<-6时, f(x)的单调递减区间为[3,-a-3] ………8分
(3)由a>0知-a-3<-3,由(2)知f(x)在[-3,3]上是减函数,又-3≤3cos ≤3,-3≤3sin
≤3,-3≤3sin ≤3,则要
≤3,则要 恒成立只要|f(-3)-f(3)|<72恒成立………10分
恒成立只要|f(-3)-f(3)|<72恒成立………10分
又|f(-3)-f(3)|=18|a+2|<72,得-6<a<2,又a>0,则0<a<2………12分
22.解:
(1)由题意设椭圆方程为 ………1分
………1分
则 ,椭圆方程为
,椭圆方程为 ………4分
………4分
(2)设 ,
,
则 ………7分
………7分
又 则
则
 ………9分
………9分
则 =
=
 ………11分
………11分
由于 ,
,

因此 的取值范围为
的取值范围为 ………14分
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com