
题目列表(包括答案和解析)
如图所示,在半径为a的圆形区域内充满磁感应强度大小为B的均匀磁场,其方向垂直于纸面向里.在圆形区域平面内固定放置一绝缘材料制成的边长为L=1.2a的刚性等边三角形框架△DEF,其中心O位于圆形区域的圆心.DE边上S点(DS=L/2)处有一发射带电粒子源,发射粒子的方向皆在图示平面内且垂直于DE边,发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值.若这些粒子与三角形框架的碰撞均无机械能损失,并要求每一次碰撞时速度方向垂直于被碰的边.试问:
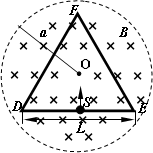
(1)若发射的粒子速度垂直于DE边向上,这些粒子中回到S点所用的最短时间是多少?
(2)若发射的粒子速度垂直于DE边向下,带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点?这些粒子中,回到S点所用的最短时间是多少?(不计粒子的重力和粒子间的相互作用)
如图所示,在半径为
a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的匀强磁场,其方向平行于轴线远离读者.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架DEF,其中心O位于圆柱的轴线上.DE边上S点(DS=L/4)有一发射带电粒子的源,发射粒子的方向皆在图中截面内且垂直于DE边向下.发射粒子的电量皆为q(q>0),质量皆为m,但速度v有各种不同的数值.若这些粒子与三角形框架的碰撞均为完全弹性碰撞,并要求每一次碰撞时速度方向垂直于被碰撞的边,问:
(1)带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点?(2)这些粒子中,回到S点所用的最短时间是多少?
(12分)电阻可忽略的光滑平行金属导轨长s=1.15 m,两导轨间距L=0.75 m,导轨倾角为30°,导轨上端ab接一阻值R=1.5 Ω的电阻,磁感应强度B=0.8 T的匀强磁场垂直轨道平面向上,如图12所示.阻值r=0.5 Ω,质量m=0.2 kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Q1=0.1 J.(取g=10 m/s2)求:
(1)金属棒在此过程中克服安培力的功W安;
(2)金属棒下滑速度v=2 m/s时的加速度a;
(3)为求金属棒下滑的最大速度vm,有同学解答如下:由动能定理,WG-W安=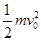 ,….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
,….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.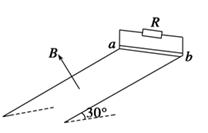
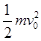 ,….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
,….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
电阻可忽略的光滑平行金属导轨长S=1.15 m,两导轨间距L=0.75 m,导轨倾角为30°,导轨上端ab接一阻值R=1.5 Ω的电阻,磁感应强度B=0.8 T的匀强磁场垂直轨道平面向上.阻值r=0.5 Ω,质量m=0.2 kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Qr=0.1 J.(取g=10 m/s2)求:

(1)金属棒在此过程中克服安培力的功![]() ;
;
(2)金属棒下滑速度v=2 m/s时的加速度a.
(3)为求金属棒下滑的最大速度vm,有同学解答如下:由动能定理![]() ,…….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
,…….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com