练习册

  • 练习册
  • 试题
    如图9.AB∥CD.AE交CD于点F.点G在AB上.GH⊥BF.垂足为H,∠1=∠2.直线AE与BF垂直吗?给下面的推理过程填空或填写理由. 解:∵ AB∥CD. ∴ ∠1=∠ ( ). ∵ ∠1=∠2,,∴ ∠ =∠ ( ), ∴ ∥ ( ).又 ∵ GH⊥BF( ).∴ ∠AFB=∠GHB=90°( ). ∴ ⊥ . 【查看更多】

     

    题目列表(包括答案和解析)

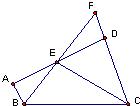    26、如图，AB∥CD，BE、CE分别是∠ABC、∠BCD的平分线，点E在AD上，BE的延长线交CD的延长线于F．求证：（1）AE=ED；（2）BC=AB+CD．

    查看答案和解析>>

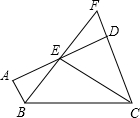    如图，AB∥CD，BE、CE分别是∠ABC、∠BCD的平分线，点E在AD上，BE的延长线交CD的延长线于F．求证：（1）AE=ED；（2）BC=AB+CD．

    查看答案和解析>>

    如图，AB//CD,∠CAB=108°，AC=2.

    ⑴用直尺和圆规作∠A的平分线AE,交CD于E,并在AB上取一点F，使AC=AF，再连接CF,交AE于K；

    （要求保留作图痕迹，不必写出作法）

    ⑵依据现有条件，直接写出图中所有相似的三角形，并求出AK.（图中不再增加字母和线段，不要求证明）.

     


    查看答案和解析>>

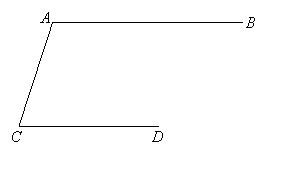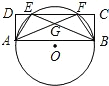    精英家教网如图，AB是⊙O的弦，矩形ABCD的边CD与⊙O交于点E，F，AF和BE相交于点G，连接AE，BF．
    （1）写出图中每一对全等的三角形（不再添加辅助线）；
    （2）选择你在（1）中写出的全等三角形中的任意一对进行证明．

    查看答案和解析>>

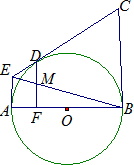    精英家教网如图，AB是⊙O的直径，CB、CD分别切⊙O于B、D两点，点E在CD的延长线上，且CE=AE+BC；
    （1）求证：AE是⊙O的切线；
    （2）过点D作DF⊥AB于点F，连接BE交DF于点M，求证：DM=MF．

    查看答案和解析>>

    一、DCCAB  DABBC

    二、11. 2,4        12. x4+2x3y-3x2+xy-5        13. 4x2+y2-4xy, 2x-y 

    14. 11,3n+2     15. 2.306×109(或2.306×105万)     16. 107     17. 115

    18. 答案不惟一（如∠FEC=∠B，∠DFE+∠FDB=180°…）

    三、19．（1）原式=-15+25-18                   ………………………………（3分）

                =-8                                ………………………………（6分）

           （2）原式=             ………………………………（2分）

                =-4-3+1                   ………………………………（4分）

                =-6                       ………………………………（6分）

        20．原式     ………………………………（2分）

                                        ………………………………（4分）

            当，时，原式   ……………（5分）

                                     =-10+4        ………………………………（6分）

                                     =-6           ………………………………（7分）

    21．（1）卡上显示金额为：1.2(x-10)或1.2x-12；   …………………………（4分）

    （2）当x=2时，1.2(x-10)=(200-10)×1.2-10=228(元).

                ∴ 卡上显示金额应为228元.                     ………………（7分）

    22．（1）过C点画直线CD∥AB正确.           ………………………………（2分）

    过C点画直线CE⊥AB于E正确.       ………………………………（4分）

    （2）画正方形ABCD正确.                 ………………………………（6分）

         正方形ABCD的面积是20cm2.          ………………………………（8分）

    （3）d, a                               ………………………………（10分）

    23. ∵ AB∥CD（ 已知 ），                  

    ∴ ∠1=∠A（ 两直线平行，内错角相等 ）.  ……………………………（2分）

    ∵ ∠1=∠2（ 已知 ）,

    ∴ ∠2=∠A （ 等量代换 ）,             ………………………………（4分）

    ∴ AE∥GH（ 同位角相等, 两直线平行 ）. ………………………………（7分）

    又∵ GH⊥BF（ 已知 ）

    ∴ ∠AFB=∠GHB=90°，（两直线平行，同位角相等 ）  …………………（9分）

    ∴ AE⊥BF.                            ………………………………（10分）

    24．（1）画图正确.                          ………………………………（2分）

    （2）316, 165, 38.6, 139, 13.6 ( 注：每空1分，共5分)      ……（7分）

    （3）图10.1, 条形统计图，能清楚地表示每个国家代表队在这届运动会上获得金牌的具体数目. 图10.2, 扇形统计图，能清楚地表示各个国家代表队这届运动会上获得金牌数在总金牌数中所占的百分比.   …………………（10分）

     


    同步练习册答案