
题目列表(包括答案和解析)
设 是定义在
是定义在 上的奇函数,当
上的奇函数,当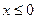 时,
时, ,则
,则
A. | B. | C.1 | D.3 |
平面向量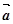 与
与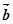 之间的夹角为
之间的夹角为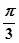 ,
,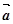 =(2,0),|
=(2,0),|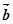 |=1,则|
|=1,则| |=(
)
|=(
)
A. B.
B. C.4
D.12
C.4
D.12
在等差数列 中,若
中,若 ,则
,则 的值为( )
的值为( )
A. 6 B. 8 C. 10 D. 16
第Ⅱ卷 (非选择题 共100分)
已知![]() 均为正数,
均为正数,![]() ,则
,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上。
已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A,B两点,且AB的中点为N(-12,-15),则E的方程为
(A)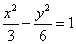 (B)
(B)  (C)
(C)
 (D)
(D)

第Ⅱ卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须做答。第(22)题~第(24)题为选考题,考生根据要求做答。
一、选择题(本大题12小题,每小题5分,共60分。在每小题经出的四个选项中,只有一项是符合题目要求的。))
1―5DCBAC 6―10BCADB 11―12BB
二、填空题(本大题共4个小题,每小题5分,共20分。将符合题意的答案填在题后的横线上)
13.2 14.70 15. 16.
16.
三、解答题:本大题共6个小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.解:(I) …………4分
…………4分


 …………6分
…………6分
(II)


 …………8分
…………8分


 …………10分
…………10分
18.解:(I)设通晓英语的有 人,
人,
且 …………1分
…………1分
则依题意有:
 …………3分
…………3分
所以,这组志愿者有 人。…………4分
人。…………4分
(II)所有可能的选法有 种…………5分
种…………5分
A被选中的选法有 种…………7分
种…………7分
A被选中的概率为 …………8分
…………8分
(III)用N表示事件“B,C不全被选中”,则 表示事件“B,C全被选中”……10分
表示事件“B,C全被选中”……10分
则 …………11分
…………11分
所以B和C不全被选中的概率为 ……12分
……12分
说明:其他解法请酌情给分。
|