(Ⅱ)判定函数()= 是否为闭函数?并说明理由, 【查看更多】

若函数f（x）同时满足下列两个性质，则称其为“规则函数”
①函数f（x）在其定义域上是单调函数；
②在函数f（x）的定义域内存在闭区间[a，b]使得f（x）在[a，b]上的最小值是

a

2

，且最大值是

b

2

．
请解答以下问题：
（Ⅰ）判断函数f（x）=x²-2x，（x∈（0，+∞））是否为“规则函数”？并说明理由；
（Ⅱ）判断函数g（x）=-x³是否为“规则函数”？并说明理由．若是，请找出满足②的闭区间[a，b]；
（Ⅲ）若函数h(x)=

x-1

+t是“规则函数”，求实数t的取值范围．

查看答案和解析>>

给出函数封闭的定义：若对于定义域D内的任意一个自变量x₀，都有函数值f（x₀）∈D，称函数y=f（x）在D上封闭．
（1）若定义域D₁=（0，1），判断函数g（x）=2x-1是否在D₁上封闭，并说明理由；
（2）若定义域D₂=（1，5]，是否存在实数a，使得函数f(x)=

5x-a

x+2

在D₂上封闭？若存在，求出a的取值范围；若不存在，请说明理由．
（3）利用（2）中函数，构造一个数列{x_n}，方法如下：对于给定的定义域D₂=（1，5]中的x₁，令x₂=f（x₁），x₃=f（x₂），…，x_n=f（x_n-1），…在上述构造数列的过程中，如果x_i（i=1，2，3，4…）在定义域中，构造数列的过程将继续下去；如果x_i不在定义域中，则构造数列的过程停止．
①如果可以用上述方法构造出一个无穷常数列{x_n}，求实数a的取值范围．
②如果取定义域中任一值作为x₁，都可以用上述方法构造出一个无穷数列{x_n}，求实数a的取值范围．

查看答案和解析>>

已知函数y=f（x），x∈D，如果对于定义域D内的任意实数x，对于给定的非零常数m，总存在非零常数T，恒有f（x+T）＞m•f（x）成立，则称函数f（x）是D上的m级类增周期函数，周期为T．若恒有f（x+T）=m•f（x）成立，则称函数f（x）是D上的m级类周期函数，周期为T．
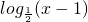（1）试判断函数f（x）= $数学公式$ 是否为（3，+∞）上的周期为1的2级类增周期函数？并说明理由；
（2）已知函数f（x）=-x²+ax是[3，+∞）上的周期为1的2级类增周期函数，求实数a的取值范围；
（3）下面两个问题可以任选一个问题作答，如果你选做了两个，我们将按照问题（Ⅰ）给你记分．
（Ⅰ）已知T=1，y=f（x）是[0，+∞）上m级类周期函数，且y=f（x）是[0，+∞）上的单调递增函数，当x∈[0，1）时，f（x）=2^x，求实数m的取值范围．
（Ⅱ）已知当x∈[0，4]时，函数f（x）=x²-4x，若f（x）是[0，+∞）上周期为4的m级类周期函数，且y=f（x）的值域为一个闭区间，求实数m的取值范围．

查看答案和解析>>

给出函数封闭的定义：若对于定义域D内的任意一个自变量x₀，都有函数值f（x₀）∈D，称函数y=f（x）在D上封闭．
（1）若定义域D₁=（0，1），判断函数g（x）=2x-1是否在D₁上封闭，并说明理由；
（2）若定义域D₂=（1，5]，是否存在实数a，使得函数f(x)=

5x-a

x+2

在D₂上封闭？若存在，求出a的取值范围；若不存在，请说明理由．
（3）利用（2）中函数，构造一个数列{x_n}，方法如下：对于给定的定义域D₂=（1，5]中的x₁，令x₂=f（x₁），x₃=f（x₂），…，x_n=f（x_n-1），…在上述构造数列的过程中，如果x_i（i=1，2，3，4…）在定义域中，构造数列的过程将继续下去；如果x_i不在定义域中，则构造数列的过程停止．
①如果可以用上述方法构造出一个无穷常数列{x_n}，求实数a的取值范围．
②如果取定义域中任一值作为x₁，都可以用上述方法构造出一个无穷数列{x_n}，求实数a的取值范围．

查看答案和解析>>

对于函数

（

，D是此函数的定义域），若同时满足下列条件：
①

在D内单调递减或单调递增；
②存在区间[a，b]

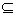D，使

在[a，b]上的值域为[a，b]；
那么把

叫闭函数；
（1）求闭函数

符合条件②的区间[a，b]；
（2）判断函数

是否为闭函数？并说明理由；
（3）

是闭函数，求实数k的取值范围。

查看答案和解析>>

一．选择题：

1．B 2．D 2．B 3．C 4．C　5． A 6．C 7．B 8．A 9．D 10．D

二．填空题：

11．a+b 12．{x|x>2, 或0<x<1} 13．4，或－1 14． 15．120º 16．②④

三．解答题：

17．由题设，得，，，双曲线为， …… 2分

直线AB的方程为， ……………………… 4分

代入到双曲线方程得：4x²+20ax-29a²=0， ……………………… 6分

又，由得：

12=， ……………………… 9分

解得a²=1，则b²=3，所以为所求。……………………… 12分

18．解：（Ⅰ）由题设可得 f '(x)=3x²+2ax+b， ……………………… 2分

∵ f '(x)的图像过点（0，0），（2，0）

∴ ……………………… 5分

解之得：a=－3，b=0 ……………………… 7分

（Ⅱ）由f '(x)=3x²－6x＞0，得x＞2，或x＜0； ……………………… 9分

∴ 当在（－∞，0）上,在(0,2)上,在上,

故在（-∞0）,上递增,在(0,2)上递减,

因此在x=2处取得极小值,所以x₀=2， ……………………… 12分

由f (2)=－5，得c=－1，

∴f（x）=x³－3x²－1 ……………………… 14分

19．：解法一：

(Ⅰ) 过P作MN∥B₁C₁，分别交A₁B₁、D₁C₁于M、N，则M、N A₁B₁、D₁C₁的中点，连MB，NC由四边形BCNM是平行四边形， ……………………… 2分

∵E、M分别为AB、A₁B₁中点，∴A₁E∥MB

又MB平面PBC，∴A₁E∥平面PBC。 ……………………… 4分

(Ⅱ) 过A作AF⊥MB，垂足为F，连PF，

∵BC⊥平面ABB₁A₁，AF平面ABB₁A₁，

∴AF⊥BC， BC∩MB=B，∴AF⊥平面PBC，

∴∠APF就是直线AP与平面PBC所成的角， ………… 6分

设AA₁=a，则AB=a，AF=，AP=，sin∠APF=

所以，直线AP与平面PBC所成的角是arcsin。 ………… 9分

（Ⅲ）连OP、OB、OC，则OP⊥BC，由三垂线定理易得OB⊥PC，OC⊥PB，所以O在平面PBC中的射影是△PBC的垂心，又O在平面PBC中的射影是△PBC的重心，则△PBC为正三角形。即PB=PC=BC ………… 12分

所以k=。

反之，当k=时，PA=AB=PB=PC=BC，所以三棱锥为正三棱锥，

∴O在平面PBC内的射影为的重心 ………… 14分

解法二：（建立空间坐标系）

20．解 (Ⅰ)由=³在[a ，b]上为减函数，

得可得a = ?1 ， b = 1 ，∴ 所求区间是[?1，1]． ………… 5分

(Ⅱ)取₁ = 1 ， ₂ = 10，可得()不是减函数；取₁ =，可得()在(0 ， +∞)不是增函数，所以()不是闭函数． ………… 10分

(Ⅲ)设函数符合条件②的区间为[a ，b]，则

故a ， b是方程=的两个实根，命题等价于

有两个不等实根． ………… 13分

当k时，解得：，∴ ；

当时，这时无解．

所以 k的取值范围是． ………… 16分

21．解：(Ⅰ)由f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，所以

x³+ax²+bx+c+(2－x)³+a(2－x)²+b(2－x)+c=2 ………… 3分

对一切实数x恒成立．得：a=－3，b+c=3，

对由f '(1)=0，得b=3，c=0，

故所求的表达式为：f(x)= x³－3x²+3x． ………… 7分

(Ⅱ) a_n₊₁=f (a_n)= a_n³－3 a_n²+3 a_n (1)

令b_n=a_n－1，0<b_n<1，由代入(1)得：b_n₊₁=，b_n=，………… 10分

∴ 1＞b_n ＞b_n₊₁＞0

(a₁－a₂)?(a₃－1)+(a₂－a₃)?(a₄－1)+…+(a_n－a_n₊₁)?(a_n₊₂－1)=

＜=b₁-b_n₊₁＜b₁＜1。 ………… 14分

（本题证法较多，其它证明方法得分可参照以上评分标准分步给分）

参考答案

一．选择题：

1．B 2．D 2．B 3．C 4．C　5． A 6．C 7．B 8．A 9．D 10．D

二．填空题：

11．a+b 12．{x|x>2, 或0<x<1} 13．4，或－1 14． 15．120º 16．②④

三．解答题：

17．由题设，得，，，双曲线为， …… 2分

直线AB的方程为， ……………………… 4分

代入到双曲线方程得：， ……………………… 6分

又，由得：

， ……………………… 9分

解得，则，所以为所求。……………………… 12分

18．解：（Ⅰ）由题设可得 f '(x)=3x²+2ax+b， ……………………… 2分

∵ f '(x)的图像过点（0，0），（2，0）

∴ ……………………… 5分

解之得：a=－3，b=0 ……………………… 7分

（Ⅱ）由f '(x)=3x²－6x＞0，得x＞2，或x＜0； ……………………… 9分

∴ 当在（－∞，0）上,在(0,2)上,在上,

故在（－∞，0）,上递增,在(0,2)上递减,

因此在x=2处取得极小值,所以x₀=2， ……………………… 12分

由f (2)=－5，得c=－1，

∴f（x）=x³－3x²－1 ……………………… 14分

19．：解法一：

(Ⅰ) 过P作MN∥B₁C₁，分别交A₁B₁、D₁C₁于M、N，则M、N A₁B₁、D₁C₁的中点，连MB，NC由四边形BCNM是平行四边形， ……………………… 2分

∵E、M分别为AB、A₁B₁中点，∴A₁E∥MB

又MB平面PBC，∴A₁E∥平面PBC。 ……………………… 4分

(Ⅱ) 过A作AF⊥MB，垂足为F，连PF，

∵BC⊥平面ABB₁A₁，AF平面ABB₁A₁，

∴AF⊥BC， BC∩MB=B，∴AF⊥平面PBC，

∴∠APF就是直线AP与平面PBC所成的角， ………… 6分

设AA₁=a，则AB=a，AF=，AP=，sin∠APF=

所以，直线AP与平面PBC所成的角是arcsin。 ………… 9分

（Ⅲ）连OP、OB、OC，则OP⊥BC，由三垂线定理易得OB⊥PC，OC⊥PB，所以O在平面PBC中的射影是△PBC的垂心，又O在平面PBC中的射影是△PBC的重心，则△PBC为正三角形。即PB=PC=BC ………… 12分

所以k=。

反之，当k=时，PA=AB=PB=PC=BC，所以三棱锥为正三棱锥，

∴O在平面PBC内的射影为的重心 ………… 14分

解法二：（建立空间坐标系）

20．解 (Ⅰ)由=³在[a ，b]上为减函数，

得可得a = ?1 ， b = 1 ，∴ 所求区间是[?1，1]． ………… 5分

(Ⅱ)取₁ = 1 ， ₂ = 10，可得()不是减函数；取₁ =，可得()在(0 ， +∞)不是增函数，所以()不是闭函数． ………… 10分

(Ⅲ)设函数符合条件②的区间为[a ，b]，则

故a ， b是方程=的两个实根，命题等价于

有两个不等实根． ………… 13分

当k时，解得：，∴ ；

当时，这时无解．

所以 k的取值范围是． ………… 16分

21．解：(Ⅰ)由f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，所以

x³+ax²+bx+c+(2－x)³+a(2－x)²+b(2－x)+c=2 ………… 3分

对一切实数x恒成立．得：a=－3，b+c=3，

对由f '(1)=0，得b=3，c=0，

故所求的表达式为：f(x)= x³－3x²+3x． ………… 7分

(Ⅱ) a_n₊₁=f (a_n)= a_n³－3 a_n²+3 a_n (1)

令b_n=a_n－1，0<b_n<1，由代入(1)得：b_n₊₁=，b_n=，………… 10分

∴ 1＞b_n ＞b_n₊₁＞0

(a₁－a₂)?(a₃－1)+(a₂－a₃)?(a₄－1)+…+(a_n－a_n₊₁)?(a_n₊₂－1)=

＜=b₁-b_n₊₁＜b₁＜1。 ………… 14分

（本题证法较多，其它证明方法得分可参照以上评分标准分步给分）

练习册

高中

初中

小学