练习册

  • 练习册
  • 试题
    (1)求 【查看更多】

     

    题目列表(包括答案和解析)

    已知：
    a
    =(cos
    3
    2
    x，sin
    3
    2
    x)，
    b
    =(cos
    x
    2
    ，sin
    x
    2
     )，x∈[
    π
    2
    ，
    3π
    2
    ]
    （1）求：|
    a
    +
    b
    |    的取值范围；
    （2）求：函数f(x)=2sinx+|
    a
    +
    b
     |    的最小值．

    查看答案和解析>>

    已知数列an的前n项和Sn满足条件2Sn=3（an-1），其中n∈N*．
    （1）求证：数列an成等比数列；
    （2）设数列bn满足bn=log3an．若 tn=
    1bnbn+1
    ，求数列tn的前n项和．

    查看答案和解析>>

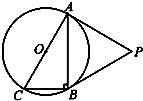    精英家教网如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
    （1）求证：PB是⊙O的切线；
    （2）已知PA=
    		3
    ，BC=1，求⊙O的半径．

    查看答案和解析>>

    设函数f（x）=cos（2x+
    π
    3
    ）+sin2x．
    （1）求函数f（x）的最大值和最小正周期．
    （2）设A，B，C为△ABC的三个内角，若cosB=
    1
    3
    ，f（
    C
    3
    ）=-
    1
    4
    ，且C为非钝角，求sinA．

    查看答案和解析>>

    在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q1为0.25，在B处的命中率为q2，该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为：
    ξ 0 2   3 4 5
     p 0.03   0.24 0.01 0.48 0.24
    （1）求q2的值；
    （2）求随机变量ξ的数学期望Eξ；
    （3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小．

    查看答案和解析>>

     

    一、选择题（共60分）

    1―6DDBBAC  7―12DABCAC

    二、填空题：（本大题共5小题，每小题5分，共20分）

    13．3

    14．

    15．

    16．240

    三、解答题：本大题有6小题，共70分，解答应写出文字说明，证明过程或演算步骤。

    17．解：（1）

              1分

          

              5分

       （2）

              7分

           由余弦定理   9分

               10分

    18．（1）记“这名考生通过书面测试”为事件A，则这名考生至少正确做出3道题，即正确做出3道题或4道题，

           故   4分

       （2）由题意得的所有可能取值分别是0，1，2，3，4，且

     

          

          

              8分

          

           的分布列为：

          

    0

    1

    2

    3

    4

    P

              10分

              12分

    19．解法一：（1）在直平行六面体ABCD―A1B1C1D1中，

          

           又

              4分

           又

       （2）如图，连B1C，则

           易证∽

           中点，

          

              8分

           取CD中点M，连BM， 则平面CC1D1D，

           作于N，连NB，由三垂线定理知：

           是二面角B―DE―C的平面角     10分

           在

          

           则二面角B―DE―C的大小为    12分

           解法二：（1）以D为坐标原点，射线DA为轴，建立如图所示坐标为

           依题设

          

          

           又

           平面BDE    6分

           8分

           由（1）知平面BDE的一个法向量为

           取DC中点M，则

          

          

           等于二面角B―DE―C的平面角    10分

              12分

    20．解：（1）由已知得   2分

           由

          

           递减

           在区间[-1，1]上的最大值为   4分

           又

          

           由题意得

           故为所求         6分

       （2）解：

          

               8分

           二次函数的判别式为：

          

           令

           令    10分

          

           为单调递增，极值点个数为0    11分

           当=0有两个不相等的实数根，根据极值点的定义，可知函数有两个极值点    12分

    21．解：（1）设

           化简得    3分

       （2）将    4分

           法一：两点不可能关于轴对称，

           的斜率必存在

           设直线DE的方程为

           由   5分

               6分

              7分

           且

              8分

           将代化入简得

              9分

           将，

           过定点（-1，-2）    10分

           将，

           过定点（1，2）即为A点，舍去     11分

               12分

           法二：设    （5分）

           则   6分

           同理

           由已知得   7分

           设直线DE的方程为

           得   9分

              10分

           即直线DE过定点（-1，-2）    12分

    22．解：（1）由    2分

           于是

           即    3分

           有   5分

              6分

       （2）由（1）得    7分

           而

          

                   

               10分

           当

           于是

           故命题得证     12分


    同步练习册答案